题目内容
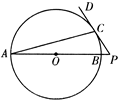 (1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=
(1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=(2)在极坐标系中,点(2,
| π | 2 |
分析:(1)连接OC,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.圆O半径为
,OP=2,所以PB=2-
,PA=2+
,PC2=PB•PA=1,PC=1.在Rt△OCP中,由∠OCP=90°,PC=1,OP=2,知∠COP=30°,由此能求出∠ACD的大小.
(2)在直角坐标系中,求出A的坐标以及A关于直线l的对称点B(2,2),由|OB|=2
,OB直线的倾斜角等于
,且点B 在第一象限,写出B的极坐标,即为所求.
| 3 |
| 3 |
| 3 |
(2)在直角坐标系中,求出A的坐标以及A关于直线l的对称点B(2,2),由|OB|=2
| 2 |
| π |
| 4 |
解答: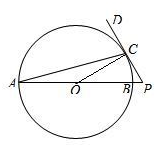 解:(1)连接OC,
解:(1)连接OC,
∵AB是圆O的直径,P在AB的延长线上,
PD切圆O于点C.圆O半径为
,OP=2,
∴PB=2-
,PA=2+
,
∴PC2=PB•PA
=(2-
)(2+
)=1,
∴PC=1.
在Rt△OCP中,
∵∠OCP=90°,PC=1,OP=2,
∴∠COP=30°,
∴∠OCA=15°,
∴∠ACD=90°-15°=75°.
故答案为:1,75°.
(2)解:在直角坐标系中,A( 0,2),直线l:x=1,A关于 直线l的对称点B(2,2).
由于|OB|=2
,OB直线的倾斜角等于
,且点B 在第一象限,
故B的极坐标为(2
,
),
故答案为(2
,
).
 解:(1)连接OC,
解:(1)连接OC,∵AB是圆O的直径,P在AB的延长线上,
PD切圆O于点C.圆O半径为
| 3 |
∴PB=2-
| 3 |
| 3 |
∴PC2=PB•PA
=(2-
| 3 |
| 3 |
∴PC=1.
在Rt△OCP中,
∵∠OCP=90°,PC=1,OP=2,
∴∠COP=30°,
∴∠OCA=15°,
∴∠ACD=90°-15°=75°.
故答案为:1,75°.
(2)解:在直角坐标系中,A( 0,2),直线l:x=1,A关于 直线l的对称点B(2,2).
由于|OB|=2
| 2 |
| π |
| 4 |
故B的极坐标为(2
| 2 |
| π |
| 4 |
故答案为(2
| 2 |
| π |
| 4 |
点评:(1)本题考查圆的切割线定理的应用,是基础题.解题时要认真审题,仔细解答,注意与圆有关的比例线段的灵活运用.
(2)本题主要考查极坐标方程与直角坐标方程的互化,用点的极坐标刻画点的位置,求出点B的直角坐标,是解题的关键.
(2)本题主要考查极坐标方程与直角坐标方程的互化,用点的极坐标刻画点的位置,求出点B的直角坐标,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 20、如图,AB是圆O的直径,C是圆周上一点,PA⊥平面ABC.
20、如图,AB是圆O的直径,C是圆周上一点,PA⊥平面ABC. 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点. (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲] 选修4-1几何证明
选修4-1几何证明