题目内容
（2013•盐城二模）（选修4-1：几何证明选讲）如图，AB是⊙O的直径，C、E为⊙O上的点，且CA平分∠BAE，DC是⊙O的切线，交AE的延长线于点D．求证：CD⊥AE．
分析：连接OC，利用圆的性质可得∠OAC=∠OCA，再利用角平分线的性质可得∠EAC=∠OCA，利用平行线的判定定理可得OC∥AD．利用切线的性质可得CD⊥OC，进而证明结论．
解答：
证明：连接OC，则∠OAC=∠OCA，
又∵CA平分∠BAE，∴∠OAC=∠EAC，
于是∠EAC=∠OCA，∴OC∥AD．
又∵DC是⊙O的切线，
∴CD⊥OC，
∴CD⊥AE．
证明：连接OC，则∠OAC=∠OCA，又∵CA平分∠BAE，∴∠OAC=∠EAC，
于是∠EAC=∠OCA，∴OC∥AD．
又∵DC是⊙O的切线，
∴CD⊥OC，
∴CD⊥AE．
点评：熟练掌握圆的性质、角平分线的性质、平行线的判定定理、圆的切线的性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
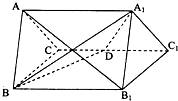（2013•盐城二模）正三棱柱ABC-A1B1C1的所有棱长都为4，D为的CC1中点．