题目内容
已知正方形ABCD和矩形ACEF所在平面互相垂直,(1) 求证:AM∥平面BDE;
(2) 求二面角A—DF—B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角为![]()
![]()
答案:
解析:
解析:
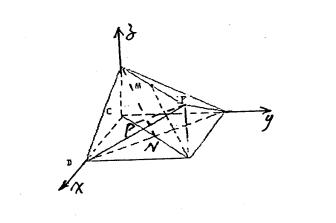
| (1)取C为坐标原点,为圆建立空间直角坐标系C-XYZ
设 则
又
(2)
即所求二面角 (1)
设
解得 即点P是AC的中点。 |

练习册系列答案
相关题目
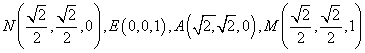
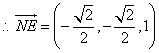
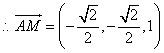
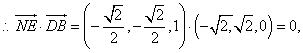
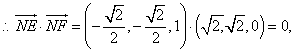
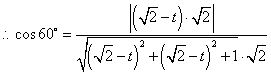
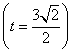 舍去。
舍去。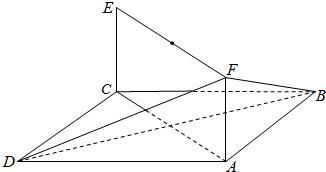 如图,已知正方形ABCD和矩形ACEF,EC⊥平面ABCD.AB=1,AF=1,
如图,已知正方形ABCD和矩形ACEF,EC⊥平面ABCD.AB=1,AF=1,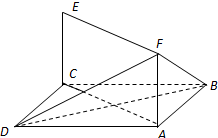 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直, 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=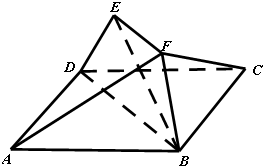 (2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,
(2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,