题目内容
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
(1)证明:CM∥平面DFB
(2)求异面直线AM与DE所成的角的余弦值.
分析:(1)设正方形的对角线AC和BD相交于点O,由条件证明MF和CO平行且相等,四边形COFM为平行四边形,故CM∥OF,再由直线和平面平行的判定定理证得 CM∥平面DFB.
(2)建立空间直角坐标系,求得点C、点A、点E、,点D、点M的坐标,可得
和
的坐标,以及|
|、|
|和
•
的值.再利用两个向量的夹角公式求得
、
的夹角θ 的余弦值,再取绝对值,即得所求.
(2)建立空间直角坐标系,求得点C、点A、点E、,点D、点M的坐标,可得
| AM |
| DE |
| AM |
| DE |
| AM |
| DE |
| AM |
| DE |
解答:解:(1)设正方形的对角线AC和BD相交于点O,∵M为的中点,ACEF为矩形,故MF和CO平行且相等,
故四边形COFM为平行四边形,故CM∥OF,
而OF?平面DFB,CM不在平面DFB内,∴CM∥平面DFB.
(2)以点C为原点,CD为x轴,CB为y轴,CE为z轴,建立空间直角坐标系,则点C(0,0),点A(
,
,0),点E(0,0,1),
点D(
,0,0),点M(
,
,1),
∴
=(-
,-
,1),
=(-
,0,1),|
|=
,|
|=
,
•
=1+0+1=2.
设
、
的夹角为θ,cosθ=
=
=
,故异面直线AM与DE所成的角的余弦值为
.
故四边形COFM为平行四边形,故CM∥OF,
而OF?平面DFB,CM不在平面DFB内,∴CM∥平面DFB.
(2)以点C为原点,CD为x轴,CB为y轴,CE为z轴,建立空间直角坐标系,则点C(0,0),点A(
| 2 |
| 2 |
点D(
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AM |
| ||
| 2 |
| ||
| 2 |
| DE |
| 2 |
| AM |
| 2 |
| DE |
| 3 |
| AM |
| DE |
设
| AM |
| DE |
| ||||
|
| 2 | ||||
|
| ||
| 3 |
| ||
| 3 |
点评:本题主要考查直线和平面平行的判定定理的应用,求异面直线所成的角的余弦值,两个向量的夹角公式的应用,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目

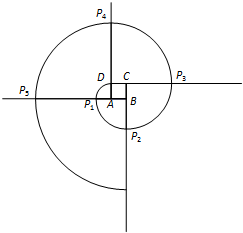 (2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
(2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是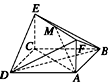
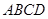 和矩形
和矩形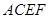 所在的平面互相垂直,
所在的平面互相垂直,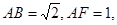
 是线段
是线段 的中点。
的中点。
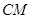 ∥平面
∥平面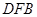
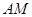 与
与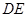 所成的角的余弦值。
所成的角的余弦值。