题目内容
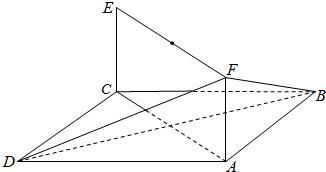 如图,已知正方形ABCD和矩形ACEF,EC⊥平面ABCD.AB=1,AF=1,
如图,已知正方形ABCD和矩形ACEF,EC⊥平面ABCD.AB=1,AF=1,(1)求证:AD⊥BF;
(2)求三棱锥C-BFD的体积.
分析:(1)证明直线与直线,先证明直线与平面垂直即要找到两条相交直线与之都垂直.在矩形ACEF中,EC∥AF,而EC⊥平面ABCD,故AF⊥面ABCD,得AF⊥AD,在正方形ABCD中AD⊥AB,所以AD⊥面AFB,可得AD⊥BF.
(2)三棱锥C-BFD的体积即三棱锥F-ABC的体积,其高为AF,底为面ABC,代入体积公式即可的其体积.
(2)三棱锥C-BFD的体积即三棱锥F-ABC的体积,其高为AF,底为面ABC,代入体积公式即可的其体积.
解答:解:(1)因为AF∥CE,
所以AF⊥ABCD,
所以AF⊥DA,又DA⊥AB,
所以DA⊥平面ABF,
所以AD⊥BF;
(2)因为VC-DBF=VF-CDB=
×
×1×1×1=
.
所以AF⊥ABCD,
所以AF⊥DA,又DA⊥AB,
所以DA⊥平面ABF,
所以AD⊥BF;
(2)因为VC-DBF=VF-CDB=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是个基础题.

练习册系列答案
相关题目
 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.