题目内容
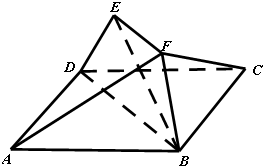 (2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,EF=BF=
(2012•江苏二模)如图,已知正方形ABCD和直角梯形BDEF所在平面互相垂直,BF⊥BD,EF=BF=| 1 | 2 |
(1)求证:DE∥平面ACF;
(2)求证:BE⊥平面ACF.
分析:(1)利用线面平行的判定证明线面平行,设AC∩BD=O,连接FO,即证明DE∥OF;
(2)利用线面垂直的判定证明线面垂直,证明BE⊥AC,BE⊥OF即可.
(2)利用线面垂直的判定证明线面垂直,证明BE⊥AC,BE⊥OF即可.
解答: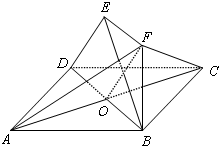 证明:(1)设AC∩BD=O,连接FO.
证明:(1)设AC∩BD=O,连接FO.
因为ABCD是正方形,所以O是BD的中点,
因为BD=2EF,所以DO∥EF且DO=EF,
所以四边形DOFE是平行四边形,
所以DE∥OF.…(5分)
因为DE?平面ACF,OF?平面AFC,所以DE∥平面ACF.…(7分)
(2)因为ABCD是正方形,所以BD⊥AC,
因为平面ABCD⊥平面BDEF,平面ABCD∩平面BDEF=BD,所以AC⊥平面BDEF,
因为BE?平面BDEF,所以BE⊥AC. …(10分)
因为BF=
BD,所以BF=BO,所以四边形BOEF是正方形,所以BE⊥OF. (12分)
因为OF∩AC=O,OF,AC?平面ACF,所以BE⊥平面ACF. …(14分)
 证明:(1)设AC∩BD=O,连接FO.
证明:(1)设AC∩BD=O,连接FO.因为ABCD是正方形,所以O是BD的中点,
因为BD=2EF,所以DO∥EF且DO=EF,
所以四边形DOFE是平行四边形,
所以DE∥OF.…(5分)
因为DE?平面ACF,OF?平面AFC,所以DE∥平面ACF.…(7分)
(2)因为ABCD是正方形,所以BD⊥AC,
因为平面ABCD⊥平面BDEF,平面ABCD∩平面BDEF=BD,所以AC⊥平面BDEF,
因为BE?平面BDEF,所以BE⊥AC. …(10分)
因为BF=
| 1 |
| 2 |
因为OF∩AC=O,OF,AC?平面ACF,所以BE⊥平面ACF. …(14分)
点评:本题考查线面平行,考查线面垂直,掌握线面平行、线面垂直的判定方法是关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (2012•江苏二模)如图,已知A、B是函数y=3sin(2x+θ)的图象与x轴两相邻交点,C是图象上A,B之间的最低点,则
(2012•江苏二模)如图,已知A、B是函数y=3sin(2x+θ)的图象与x轴两相邻交点,C是图象上A,B之间的最低点,则 (2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=
(2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=