题目内容
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=| 2 |
(1)求证:AF∥平面BDE;
(2)求证:DF⊥平面BEF;
(3)求二面角A-BF-E的余弦值.
分析:(1)利用线面平行的判定,证明AF∥EO即可;
(2)利用线面垂直的判定,证明BF⊥EF,BF⊥DF,即可证得BF⊥平面DEF;
(3)取BF中点M,BE中点N,连接AM、MN、AN,则∠AMN就是二面角A-BF-E的平面角,由此可求二面角A--BF--E的余弦值.
(2)利用线面垂直的判定,证明BF⊥EF,BF⊥DF,即可证得BF⊥平面DEF;
(3)取BF中点M,BE中点N,连接AM、MN、AN,则∠AMN就是二面角A-BF-E的平面角,由此可求二面角A--BF--E的余弦值.
解答: (1)证明:设AC与BD交与点O.
(1)证明:设AC与BD交与点O.
∵EF∥AO,且EF=1,AO=
AC=1.
∴四边形AOEF为平行四边形,
∴AF∥EO,
∵EO?面BDE,AF?面BDE,∴AF∥面BDE.…(3分)
(2)证明:∵正方形ABCD和四边形ACEF所在的平面相互垂直,且CE⊥AC,∴CE⊥面ABCD,
连接FO,∵正方形ABCD的边长为
,∴AC=BD=2;
直角梯形ACEF中,FO∥EC,且FO=1,DF=BF=
,DE=BE=
,则BF⊥EF,
由BF=DF=
,BD=2可知BF⊥DF,
∵EF∩DF=F
∴DF⊥平面BEF;…(7分)
(3)解:取BF中点M,BE中点N,连接AM、MN、AN,
∵AB=BF=AF=
,∴AM⊥BF,
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角.
AM=
AB=
,MN=
EF=
;
在Rt△APN中,可得AN2=AP2+NP2=
,
∴在△AMN中,可得cos∠AMN=
=-
,…(12分)
 (1)证明:设AC与BD交与点O.
(1)证明:设AC与BD交与点O.∵EF∥AO,且EF=1,AO=
| 1 |
| 2 |
∴四边形AOEF为平行四边形,
∴AF∥EO,
∵EO?面BDE,AF?面BDE,∴AF∥面BDE.…(3分)
(2)证明:∵正方形ABCD和四边形ACEF所在的平面相互垂直,且CE⊥AC,∴CE⊥面ABCD,
连接FO,∵正方形ABCD的边长为
| 2 |
直角梯形ACEF中,FO∥EC,且FO=1,DF=BF=
| 2 |
| 3 |
由BF=DF=
| 2 |
∵EF∩DF=F
∴DF⊥平面BEF;…(7分)
(3)解:取BF中点M,BE中点N,连接AM、MN、AN,
∵AB=BF=AF=
| 2 |
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角.
AM=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△APN中,可得AN2=AP2+NP2=
| 11 |
| 4 |
∴在△AMN中,可得cos∠AMN=
| AM2+MN2-AN2 |
| 2AM•MN |
| ||
| 3 |
点评:本题考查线面平行、线面垂直,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
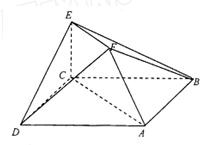 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=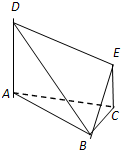 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.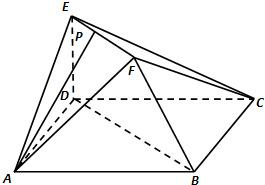 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.