题目内容
19.已知数列{an},{bn}满足a1=1,a2=2,b1=2,且对任意的正整数i,j,k,l,当i+j=k+l时都有aibj=akbl,记cn=$\root{n}{({a}_{1}+{b}_{1})({a}_{2}+{b}_{2})({a}_{3}+{b}_{3})…({a}_{n}+{b}_{n})}$,则数列{cn}的通项公式是$3×{2}^{\frac{n-1}{2}}$.分析 由已知得a2bn=a1bn+1,an+1b1=anb2,从而求出an+bn=3×2n-1,由此能求出数列{cn}的通项公式.
解答 解:∵数列{an},{bn}满足a1=1,a2=2,b1=2,
且对任意的正整数i,j,k,l,当i+j=k+l时都有aibj=akbl,
∴a2bn=a1bn+1,整理,得:$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{a}_{2}}{{a}_{1}}$=2,
∴{bn}是首项为2,公比为2的等比数列,∴bn=2n.∴b2=4,
又an+1b1=anb2,整理,得$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{b}_{2}}{{b}_{1}}$=2,
∴{an}是首项为1,公比为2的等比数列,∴an=2n-1.
∴an+bn=3×2n-1,
∴cn=$\root{n}{({a}_{1}+{b}_{1})({a}_{2}+{b}_{2})({a}_{3}+{b}_{3})…({a}_{n}+{b}_{n})}$
=$\root{n}{{3}^{n}•[{2}^{0+1+2+3+…+(n-1)}]}$
=3×${2}^{\frac{n-1}{2}}$.
∴cn=$3×{2}^{\frac{n-1}{2}}$.
故答案为:$3×{2}^{\frac{n-1}{2}}$.
点评 本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法和等比数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知数列{xn}满足xn+3=xn,xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1,a≠0)则数列{xn}的前2016项的和S2016为( )
| A. | 671 | B. | 670 | C. | 1342 | D. | 1344 |
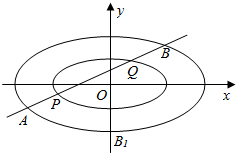 已知椭圆C1,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)与椭圆C2:$\frac{{x}^{2}}{4}$+y2=1有相同的离心率,经过点P(-2,0)的直线l与椭圆C2相交于P、Q两点,与椭圆C1相交于A、B两点.
已知椭圆C1,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)与椭圆C2:$\frac{{x}^{2}}{4}$+y2=1有相同的离心率,经过点P(-2,0)的直线l与椭圆C2相交于P、Q两点,与椭圆C1相交于A、B两点.