题目内容
已知函数 .
.
(Ⅰ) 当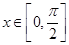 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(Ⅱ)设a,b,c分别为△ABC三个内角A,B,C的对边,f(C)=3,c=1,ab= ,求a,b的值。
,求a,b的值。
 .
. (Ⅰ) 当
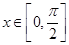 时,求函数f(x)的值域;
时,求函数f(x)的值域;(Ⅱ)设a,b,c分别为△ABC三个内角A,B,C的对边,f(C)=3,c=1,ab=
 ,求a,b的值。
,求a,b的值。(1) (2)
(2) 或
或 
 (2)
(2) 或
或 
试题分析:(Ⅰ)


∵
 ,∴
,∴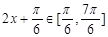 ,∴
,∴ ,
,∴函数
 的值域为
的值域为 .
. (Ⅱ)∵
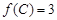 ,∴
,∴ ,即
,即 .
.∵
 ,∴
,∴ ,∴
,∴ , ∴
, ∴ .
. 又
 ,
, ,
, ,
, ,∴
,∴ .
.由
 , 得
, 得  或
或  .
. 点评:解决该试题的关键是能利用二倍角公式,将已知的函数化简为单一的三角函数,然后借助于三角函数的变量的范围,求解其值域。同时结合三角形的余弦定理,得到关于a,b的方程,求解医院二次方程得到结论。属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
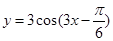 的最小正周期为 .
的最小正周期为 . 的图像与x轴的交点的横坐标构成一个公差为
的图像与x轴的交点的横坐标构成一个公差为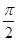 的等差数列,要得到函数
的等差数列,要得到函数 的图像,只需将
的图像,只需将 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向右平移
个单位 D.向右平移 在点
在点 处的切线方程是( )
处的切线方程是( )
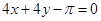


 ,
, . 记
. 记 (其中
(其中 都为常数,且
都为常数,且 ).
).  ,
,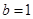 ,求
,求 的最大值及此时的
的最大值及此时的 值;
值;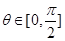 ,①证明:
,①证明: ;②证明:
;②证明: .
. 。
。 的周期和及其图象的对称中心;
的周期和及其图象的对称中心;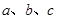 ,满足
,满足 求函数
求函数 的取值范围。
的取值范围。
 的最小正周期及单调递减区间;
的最小正周期及单调递减区间; 时,函数
时,函数 ,求不等式
,求不等式 的解集.
的解集. 中,已知
中,已知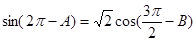 ,
, .
.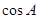 的值;
的值;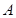 、
、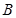 、
、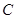 的值.
的值. 的解集是 .
的解集是 .