题目内容
已知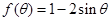 ,
,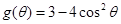 . 记
. 记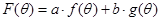 (其中
(其中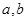 都为常数,且
都为常数,且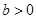 ).
).
(Ⅰ)若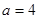 ,
,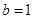 ,求
,求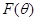 的最大值及此时的
的最大值及此时的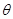 值;
值;
(Ⅱ)若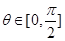 ,①证明:
,①证明: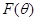 的最大值是
的最大值是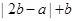 ;②证明:
;②证明: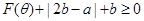 .
.
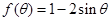 ,
,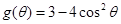 . 记
. 记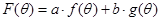 (其中
(其中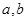 都为常数,且
都为常数,且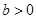 ).
). (Ⅰ)若
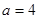 ,
,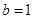 ,求
,求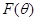 的最大值及此时的
的最大值及此时的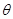 值;
值;(Ⅱ)若
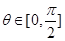 ,①证明:
,①证明: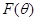 的最大值是
的最大值是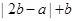 ;②证明:
;②证明: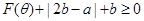 .
.(Ⅰ) ,此时的
,此时的
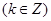 ;
;
(Ⅱ)通过令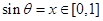 ,得到
,得到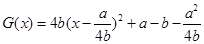
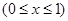
则其对称轴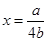 。利用二次函数图象和性质证明。
。利用二次函数图象和性质证明。
 ,此时的
,此时的
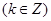 ;
; (Ⅱ)通过令
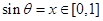 ,得到
,得到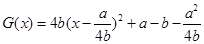
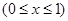
则其对称轴
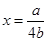 。利用二次函数图象和性质证明。
。利用二次函数图象和性质证明。试题分析:(Ⅰ)若
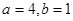 时,
时,
则
 ,此时的
,此时的
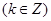 ; 6分
; 6分(Ⅱ)证明:

令
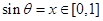 ,记
,记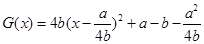
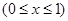
则其对称轴
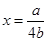
①当
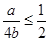 ,即
,即 时,
时,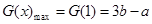
当
 ,即
,即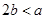 时,
时,
故
 - -11分
- -11分②即求证
 ,
,其中
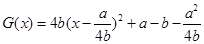
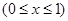
当
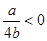 ,即
,即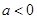 时,
时,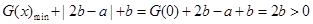
当
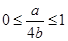 ,即
,即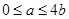 时,
时,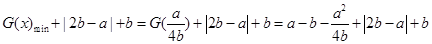
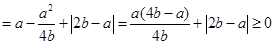
当
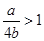 ,即
,即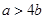 时,
时,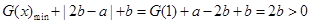
综上:
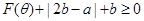 15分
15分点评:典型题,讨论二次函数型最值,往往由“轴动区间定”、“轴定区间动”的情况,要结合函数图象,分类讨论,做出全面分析。共同的是讨论二次函数图象的对称轴与区间的相对位置。本题较难。

练习册系列答案
相关题目
 的最小正周期为
的最小正周期为 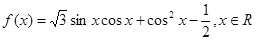
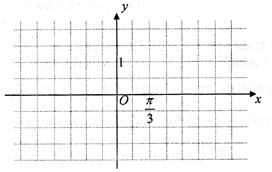
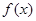 的最小正周期和单调增区间;
的最小正周期和单调增区间;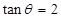 ,则
,则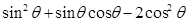 的值为 。
的值为 。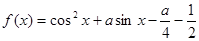 .
. ≤
≤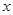 ≤
≤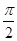 时,用
时,用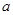 表示
表示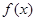 的最大值
的最大值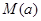 ;
;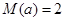 时,求
时,求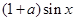 在
在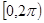 上有两解?
上有两解? .
.  时,求函数f(x)的值域;
时,求函数f(x)的值域;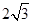 ,求a,b的值。
,求a,b的值。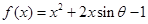 ,
,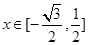
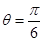 时,求
时,求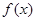 的最大值和最小值
的最大值和最小值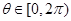 ,求
,求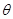 的取值范围
的取值范围 导函数的图象如图所示,则下列说法正确的是( )
导函数的图象如图所示,则下列说法正确的是( )


 处取得极大值
处取得极大值 处取得极小值
处取得极小值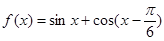 ,
,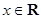 .
.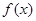 的最大值;
的最大值;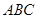 中,角
中,角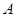 、
、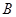 的对边分别为
的对边分别为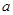 、
、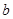 ,若
,若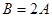 且
且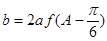 ,
,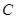 的大小.
的大小.