题目内容
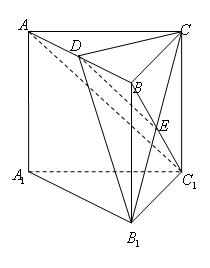
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AD⊥PD,BC=1,PC=2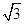 ,PD=CD=2.
,PD=CD=2.
(1)求异面直线PA与BC所成角的正切值;
(2)证明平面PDC⊥平面ABCD;
(3)求直线PB与平面ABCD所成角的正弦值.
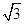 ,PD=CD=2.
,PD=CD=2.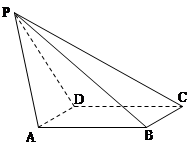
(1)求异面直线PA与BC所成角的正切值;
(2)证明平面PDC⊥平面ABCD;
(3)求直线PB与平面ABCD所成角的正弦值.
1)2
(2)证明:由于底面 是矩形,故
是矩形,故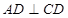 ,又由于
,又由于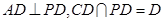 ,
,
因此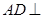 平面PDC,而
平面PDC,而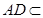 平面
平面 ,所以平面
,所以平面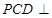 平面
平面 .
.
(3)
(2)证明:由于底面
 是矩形,故
是矩形,故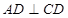 ,又由于
,又由于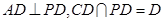 ,
,因此
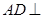 平面PDC,而
平面PDC,而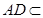 平面
平面 ,所以平面
,所以平面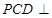 平面
平面 .
.(3)

(1)找出线面角是求解的关键,因为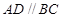 ,所以可知
,所以可知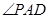 为异面直线
为异面直线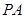 与
与 所成的角.
所成的角.
如图,

在四棱锥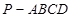 中,因为底面
中,因为底面 是矩形,
是矩形,
所以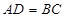 且
且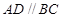 ,又因为
,又因为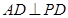 ,故
,故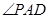 为异面直线
为异面直线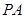 与
与 所成的角.
所成的角.
在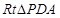 中,
中,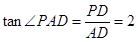 ,
,
所以,异面直线PA与BC所成角的正切值为2.
(2)证明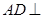 平面PDC即可.
平面PDC即可.
(3)在平面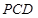 内,过点P作
内,过点P作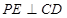 交直线CD于点E,连接EB.因为平面
交直线CD于点E,连接EB.因为平面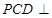 平面
平面 ,故
,故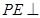 平面
平面 ,由此得
,由此得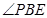 为直线PB与平面
为直线PB与平面 所成的角.余下的问题是解三角形求角.
所成的角.余下的问题是解三角形求角.
在平面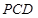 内,过点P作
内,过点P作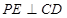 交直线CD于点E,连接EB.
交直线CD于点E,连接EB.
由于平面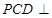 平面
平面 ,而直线CD是平面
,而直线CD是平面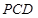 与平面
与平面 的交线,
的交线,
故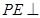 平面
平面 ,由此得
,由此得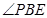 为直线PB与平面
为直线PB与平面 所成的角.
所成的角.
在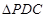 中,由于
中,由于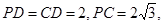 可得
可得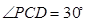 .
.
在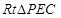 中,
中,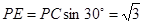 ,
,
由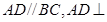 平面
平面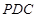 ,得
,得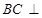 平面
平面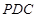 ,
,
因此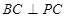 ,在
,在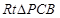 中,
中,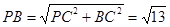 .
.
在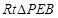 中,
中,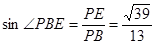
所以直线PB与平面ABCD所成的角的正弦值为 .
.
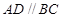 ,所以可知
,所以可知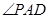 为异面直线
为异面直线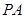 与
与 所成的角.
所成的角.如图,

在四棱锥
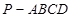 中,因为底面
中,因为底面 是矩形,
是矩形,所以
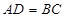 且
且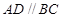 ,又因为
,又因为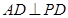 ,故
,故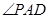 为异面直线
为异面直线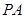 与
与 所成的角.
所成的角.在
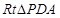 中,
中,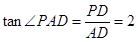 ,
,所以,异面直线PA与BC所成角的正切值为2.
(2)证明
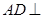 平面PDC即可.
平面PDC即可.(3)在平面
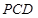 内,过点P作
内,过点P作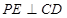 交直线CD于点E,连接EB.因为平面
交直线CD于点E,连接EB.因为平面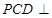 平面
平面 ,故
,故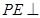 平面
平面 ,由此得
,由此得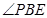 为直线PB与平面
为直线PB与平面 所成的角.余下的问题是解三角形求角.
所成的角.余下的问题是解三角形求角.在平面
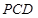 内,过点P作
内,过点P作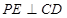 交直线CD于点E,连接EB.
交直线CD于点E,连接EB.由于平面
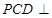 平面
平面 ,而直线CD是平面
,而直线CD是平面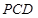 与平面
与平面 的交线,
的交线,故
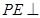 平面
平面 ,由此得
,由此得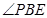 为直线PB与平面
为直线PB与平面 所成的角.
所成的角.在
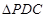 中,由于
中,由于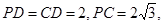 可得
可得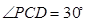 .
.在
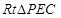 中,
中,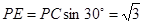 ,
,由
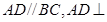 平面
平面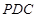 ,得
,得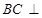 平面
平面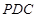 ,
,因此
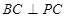 ,在
,在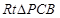 中,
中,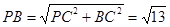 .
.在
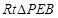 中,
中,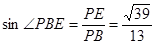
所以直线PB与平面ABCD所成的角的正弦值为
 .
.
练习册系列答案
相关题目
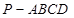 中,底面
中,底面 为平行四边形,
为平行四边形,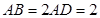 ,
,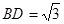 ,
,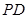 ⊥底面
⊥底面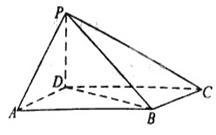
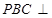 平面
平面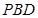 ;
; 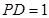 ,求
,求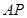 与平面
与平面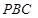 所成角
所成角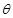 的正弦值.
的正弦值. 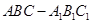 中,
中,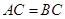 ,点
,点 是
是 的中点,
的中点,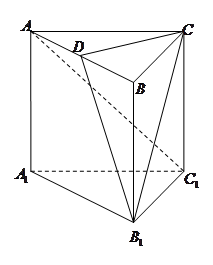
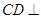 平面
平面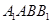 ;
;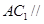 平面
平面

 是三条不同的直线,
是三条不同的直线, 是两个不同的平面,则能使
是两个不同的平面,则能使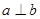 成立是( )
成立是( )
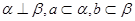
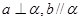
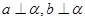
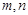 是两条不同的直线,
是两条不同的直线,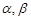 是两个不同的平面,
是两个不同的平面,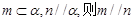 ;
;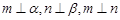 ,则
,则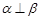 ;
;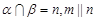 则
则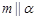 且
且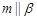 ;
;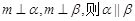
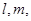 平面
平面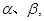 且
且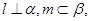 给出下列四个命题:
给出下列四个命题: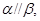 则
则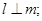 ②若
②若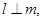 则
则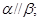
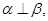 则
则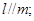 ④若
④若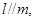 则
则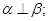
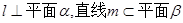 ,有下面四个命题:
,有下面四个命题: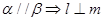 ;(2)
;(2)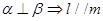 ;(3)
;(3)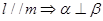 ;(4)
;(4)