题目内容
18.用数学归纳法证明(1+x)n>1+nx,这里x>-1且x≠0,n∈N*且n≥2.分析 (1)验证当n=2时,原不等式成立;(2)假设当n=k时不等式成立,由数学归纳法证明当n=k+1时不等式也成立即可.
解答 证明:(1)当n=2时,左边=1+2x+x2,右边=1+2x,
∵x2>0,∴左边>右边,原不等式成立;
(2)假设当n=k时,不等式成立,即(1+x)k>1+kx,
则当n=k+1时,∵x>-1,∴1+x>0,
在不等式(1+x)k>1+kx两边同乘以1+x得
(1+x)k•(1+x)>(1+kx)•(1+x)=1+(k+1)x+kx2>1+(k+1)x,
∴(1+x)k+1>1+(k+1)x.即当n=k+1时,不等式也成立.
综合(1)(2)可得对一切正整数n,不等式都成立.
点评 本题考查数学归纳法证明不等式,属中档题.

练习册系列答案
相关题目
10.对于任意两个自然数m,n,定义某种?运算如下:当m,n都为奇数或偶数时,m?n=m+n;当m,n中一个为偶数,另一个为奇数时,m?n=mn.则在此定义下,集合M={(a,b)|a?b=18,a∈N,b∈N}中的元素个数为( )
| A. | 26 | B. | 25 | C. | 24 | D. | 23 |
9.经过如图程序,变量y的值为( )
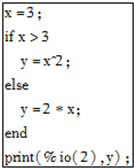
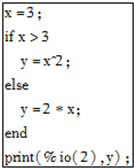
| A. | 3 | B. | 6 | C. | 9 | D. | 27 |