题目内容
(本小题共12分)
设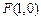 ,
,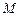 点在
点在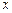 轴的负半轴上,点
轴的负半轴上,点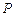 在
在 轴上,且
轴上,且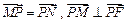 .
.
(1)当点 在
在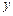 轴上运动时,求点
轴上运动时,求点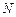 的轨迹
的轨迹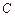 的方程;
的方程;
(2)若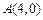 ,是否存在垂直
,是否存在垂直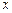 轴的直线
轴的直线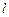 被以
被以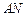 为直径的圆截得的弦长恒为定值?若存在,求出直线
为直径的圆截得的弦长恒为定值?若存在,求出直线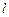 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
设
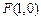 ,
,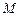 点在
点在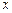 轴的负半轴上,点
轴的负半轴上,点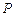 在
在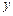 轴上,且
轴上,且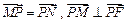 .
.(1)当点
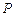 在
在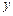 轴上运动时,求点
轴上运动时,求点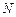 的轨迹
的轨迹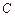 的方程;
的方程;(2)若
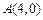 ,是否存在垂直
,是否存在垂直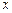 轴的直线
轴的直线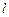 被以
被以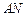 为直径的圆截得的弦长恒为定值?若存在,求出直线
为直径的圆截得的弦长恒为定值?若存在,求出直线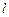 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.解:(1)(解法一)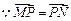 ,故
,故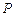 为
为 的中点.
的中点.
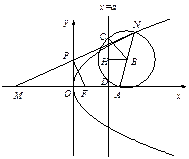
设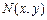 ,由
,由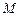 点在
点在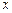 轴的负半轴上,则
轴的负半轴上,则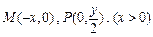
又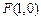 ,
,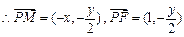
又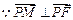 ,
,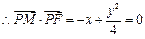
所以,点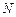 的轨迹
的轨迹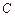 的方程为
的方程为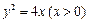
(解法二)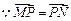 ,故
,故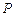 为
为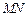 的中点. 设
的中点. 设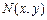 ,由
,由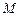 点在
点在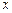 轴的负半轴上,则
轴的负半轴上,则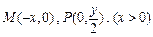 -------1分
-------1分
又由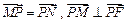 ,故
,故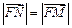 ,可得
,可得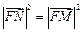 -------2分
-------2分
由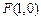 ,则有
,则有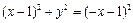 ,化简得:
,化简得: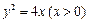
 -------3分
-------3分
所以,点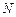 的轨迹
的轨迹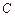 的方程为
的方程为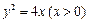 -------4分
-------4分
(2)设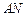 的中点为
的中点为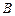 ,垂直于
,垂直于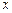 轴的直线方程为
轴的直线方程为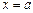 ,
,
以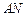 为直径的圆交
为直径的圆交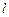 于
于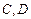 两点,
两点,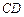 的中点为
的中点为 .
.
 ,
,
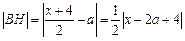 -------9分
-------9分
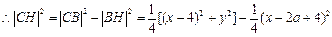
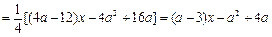 -------11分
-------11分
所以,令
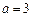 ,则对任意满足条件的
,则对任意满足条件的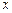 ,
,
都有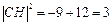 (与
(与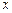 无关),即
无关),即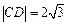 为定值. -------12分
为定值. -------12分
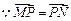 ,故
,故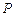 为
为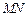 的中点.
的中点.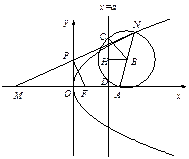
设
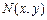 ,由
,由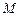 点在
点在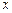 轴的负半轴上,则
轴的负半轴上,则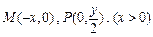
又
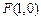 ,
,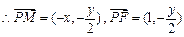
又
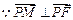 ,
,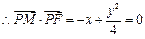
所以,点
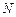 的轨迹
的轨迹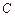 的方程为
的方程为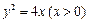
(解法二)
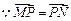 ,故
,故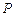 为
为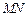 的中点. 设
的中点. 设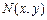 ,由
,由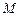 点在
点在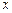 轴的负半轴上,则
轴的负半轴上,则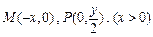 -------1分
-------1分又由
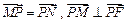 ,故
,故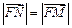 ,可得
,可得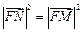 -------2分
-------2分由
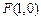 ,则有
,则有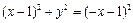 ,化简得:
,化简得: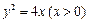
 -------3分
-------3分所以,点
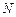 的轨迹
的轨迹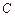 的方程为
的方程为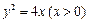 -------4分
-------4分(2)设
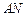 的中点为
的中点为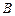 ,垂直于
,垂直于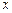 轴的直线方程为
轴的直线方程为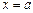 ,
,以
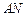 为直径的圆交
为直径的圆交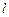 于
于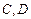 两点,
两点,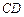 的中点为
的中点为 .
. ,
,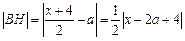 -------9分
-------9分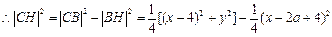
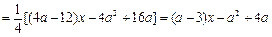 -------11分
-------11分所以,令

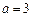 ,则对任意满足条件的
,则对任意满足条件的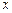 ,
,都有
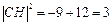 (与
(与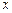 无关),即
无关),即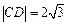 为定值. -------12分
为定值. -------12分略

练习册系列答案
相关题目
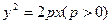 上有一点
上有一点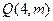 到焦点的距离为5,
到焦点的距离为5,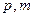 的值;
的值; 线
线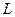 交抛物线于
交抛物线于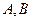 两点,求线段
两点,求线段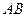 的长。
的长。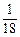 x2-
x2-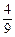 x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)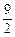 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;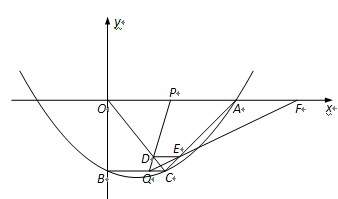
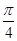 的直线
的直线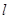 通过抛物线
通过抛物线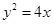 的焦点且与抛物线相交于
的焦点且与抛物线相交于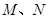 两点,则线段
两点,则线段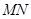 的长为
的长为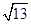
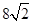
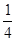 ,0)
,0)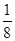 ,0)
,0)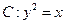 与直线
与直线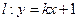 ,“
,“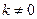 ”是“直线
”是“直线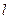 与抛物线
与抛物线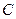 有两个不同交点”的( )
有两个不同交点”的( ) 条件
条件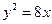 上一点
上一点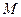 到
到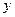 轴的距离为4,则点
轴的距离为4,则点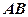 是抛物线
是抛物线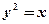 的一条焦点弦,若
的一条焦点弦,若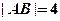 ,则
,则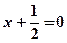 的距离为 .
的距离为 .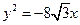 有共同焦点,且一条渐近线方程是
有共同焦点,且一条渐近线方程是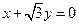 的双曲线的方程是 .
的双曲线的方程是 .