Question

【题目】已知函数的值域为，记函数.

（1）求实数的值；

（2）存在使得不等式成立，求实数的取值范围；

（3）若关于的方程有5个不等的实数根，求实数的取值范围.

Answer 1

【答案】（1）1,(2) ,(3)

【解析】

（1）利用配方法，结合二次函数的性质求得的值.

（2）将原问题转化为“存在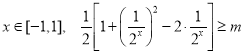成立”，利用换元法，结合二次函数的性质，求得的取值范围.

（3）首先判断不是方程的根. 当时，利用换元法，将原方程转化为.通过研究的单调性和值域，结合方程根的个数，求得的取值范围，由此求得的取值范围.

（1）因为，

即有时，，

即，解得..

（2）由已知可得，

由可转化为，存在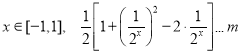成立，

令，

则问题转化为存在使不等式成立，

记，则.

（3）当，2时，，所以不是方程的根；

当时，令，

则当时，单调递减，且，

当单调递增，且，

当时，单调递减，且，

当时，单调递增，且，

故原方程有5个不等实根可转化为

即为，

所以或，

当，方程有3个不等根，

故要使得原方程有5个不等实根，只要，即，

所以的取值范围是.