Question

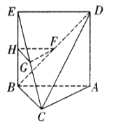
【题目】如图所示的多面体中, AC⊥BC,四边形ABED是正方形,平面ABED⊥平面ABC,点F,G,H分别为BD,EC,BE的中点,求证:

(1) BC⊥平面ACD

(2)平面HGF∥平面ABC.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）利用面面垂直的性质证得平面，得出即可；

（2）利用中位线关系证明平行于平面即可.

（1）由题：平面ABED⊥平面ABC,交线为，

四边形ABED是正方形,所以，平面ABED，

所以平面，平面，，

由题AC⊥BC, 是平面ACD内的两条相交直线，

所以BC⊥平面ACD

（2）在中分别是的中点，所以，平面，

平面，所以平面，

在中分别是的中点，所以， 所以，

平面，

平面，所以平面，是平面内两条相交直线，

所以平面HGF∥平面ABC.