题目内容
（本题满分16分）
围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用的旧墙需维修），其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为2m的进出口，如图所示已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙长度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）
⑴将y表示为x的函数；
⑵写出f(x)的单调区间，并证明；
⑶根据⑵，试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用。
【答案】
解：⑴如图，设矩形的另一边长为a m
则y=45x+180(x－2)+180×2a=225x+360a－360
由已知 ax=360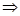
a=
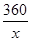
∴y=225x+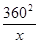
－360(x>0) ……………………………………………6′
⑵任取x1>x2>0
y1－y2=225(x1－x2)+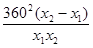
=(x1－x2)( 225－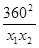
) ……………………………………10′
∴x1x2>(
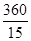)2=242时， y1>y2
x1x2<24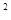
时，
y1
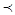y2
∴x1>x2≥24时
y1>y2 24> x1>x2>0时
y1<y2
即f(x)在（0，24）单调减，在（24，+∞）单调增 …………………14′
⑶x=24时，修建围墙的总费用最小，最小费用为10440元…………………16
【解析】略
练习册系列答案
相关题目
（
，
、
是常数，且
），对定义域内任意
（
且
），恒有
成立．
的解析式，并写出函数的定义域；
．
的前
项和为
，且
．数列
中，
，
．（1）求数列
使数列
是等比数列，求数列
；②
．
在
上的单调性；
，使
，则称
的不动点，现已知该函数有且仅有一个不动点，求
的值；
在