题目内容
16.过点P(3,0)有一条直线l,它夹在两条直线l1:2x-y-2=0与l2:x+y+3=0之间的线段恰被点P平分,则直线l方程为( )| A. | 6x-y-18=0 | B. | 8x-y-24=0 | C. | 5x-2y-15=0 | D. | 8x-3y-24=0 |
分析 当斜率不存在时,不合题意;当斜率存在时,设所求的直线方程为y=k(x-3),进而得出交点,根据点P为两交点的中点建立等式,求出k的值,从而求出所求.
解答 解:如果所求直线斜率不存在,则此直线方程为x=3,不合题意.
∴设所求的直线m方程为y=k(x-3),
∴分别联立直线m与l1,l2的方程得$\left\{\begin{array}{l}y=k(x-3)\\ x+y+3=0\end{array}\right.$与$\left\{\begin{array}{l}y=k(x-3)\\ 2x-y-2=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}x=\frac{3k-3}{k+1}\\ y=\frac{-6k}{k+1}\end{array}\right.$与$\left\{\begin{array}{l}x=\frac{3k-2}{k-2}\\ y=\frac{4k}{k-2}\end{array}\right.$,
∴直线m与l1,l2的交点分别为($\frac{3k-3}{k+1},\frac{-6k}{k+1}$),($\frac{3k-2}{k-2},\frac{4k}{k-2}$).
∵夹在两条直线l1:x+y+3=0与l2:2x-y-2=0之间的线段恰被点P平分,
∴$\frac{3k-3}{k+1}+\frac{3k-2}{k-2}=6$,且$\frac{-6k}{k+1}+\frac{4k}{k-2}=0$,
解得k=8,
∴所求的直线方程为y=8x-24.即8x-y-24=0,
故选:B.
点评 本题主要考查了直线的点斜式方程,交点坐标的求法以及中点坐标公式等知识,有一定的综合性,同时考查了运算求解的能力,属于中档题.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案| A. | (0,$\frac{\sqrt{2}}{2}$]∪[4,+∞) | B. | [$\frac{\sqrt{2}}{2}$,1)∪(1,4] | C. | ($\frac{\sqrt{2}}{2}$,1)∪(1,4) | D. | (0,$\frac{\sqrt{2}}{2}$)∪(4,+∞) |
| A. | (1+x)2=2000 | B. | 2000(1+x)2=3600 | ||
| C. | (3600-2000)(1+x)=3600 | D. | (3600-2000)(1+x)2=3600 |
| A. | -2,-3 | B. | -3,-6 | C. | -2,-6 | D. | 0,-2 |
 中,
中, ,
, ,
,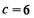 ,则
,则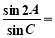 .
.