题目内容
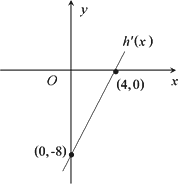
已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如下,且f(x)=ln x-h(x).
(1)求函数f(x)在x=1处的切线斜率;
(2)若函数f(x)在上是单调函数,求实数m的取值范围;
(3)若函数y=2x-lnx(x∈[1,4])的图象总在函数y=f(x)的图象的上方,求c的取值范围.
(1)由题知,h′(x)=2ax+b,其图象为直线,且过A(2,-1)、B(0,3)两点,
∴,解得. zxxk
∴h(x)=-x2+3x+c.
∴f(x)=ln x-(-x2+3x+c)=x2-3x-c+ln x.
∴f′(x)=2x-3+,
∴f′(1)=2-3+=0,
所以函数f(x)在x=1处的切线斜率为0.
(2)由题意可知,函数f(x)的定义域为(0,+∞),zxxk
由(1)知,f′(x)=2x-3+==.
令f′(x)=0,得x=或x=1.
当x变化时,f(x)、f′(x)随x的变化情况如下表:
|
x |
1 |
(1,+∞) |
|||
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
|
极小值 |
|
∴f(x)的单调递增区间为,(1,+∞).
f(x)的单调递减区间为.
要使函数f(x)在区间上是单调函数,
则,解得<m≤.
故实数m的取值范围是.
(3)由题意可知,2x-ln x>x2-3x-c+ln x在x∈[1,4]上恒成立,
即当x∈[1,4]时,c>x2-5x+2ln x恒成立
设g(x)=x2-5x+2ln x,x∈[1,4],则c>g(x)max.
易知g′(x)=2x-5+==.
令g′(x)=0得,x=或x=2. zxxk
当x∈(1,2)时,g′(x)<0,函数g(x)单调递减;当x∈(2,4)时,g′(x)>0,函数g(x)单调递增.
而g(1)=12-5×1+2ln 1=-4,g(4)=42-5×4+2ln 4=-4+4ln 2,
显然g(1)<g(4),故函数g(x)在[1,4]上的最大值为g(4)=-4+4ln 2,
故c>-4+4ln 2.
∴c的取值范围为(-4+4ln 2,+∞)
【解析】略

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案 ?
? ?
? ?
?
 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)
 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围; 的图象如图,f(x)=6lnx+h(x).
的图象如图,f(x)=6lnx+h(x).
 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;