题目内容
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)

(1)求f(x)在x=3处的切线斜率;
(2)若f(x)在区间(m,m+ )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;
(3)若对任意k∈[-1,1],函数y=kx(x∈(0,6])的图象总在函数y=f(x)图象的上方,求c的取值范围
(1)0;(2)实数m的取值范围为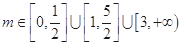 ;(3)c的取值范围
;(3)c的取值范围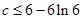
【解析】
试题分析:(1)首先根据导函数的图象可得导函数的解析式,从而求得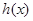 中的
中的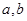 ,然后再求
,然后再求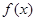 的导数,由此可得f(x)在点
的导数,由此可得f(x)在点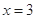 处的切线斜率 (2)
处的切线斜率 (2)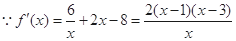 ,这里并不含参数
,这里并不含参数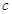 ,可以求出它的单调区间 要使 f(x)在区间(m,m+
,可以求出它的单调区间 要使 f(x)在区间(m,m+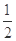 )上是单调函数,只需(m,m+
)上是单调函数,只需(m,m+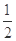 )在
)在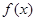 的单调区间内即可,然后通过解不等式即得m的取值范围;
的单调区间内即可,然后通过解不等式即得m的取值范围;
(3)函数y=kx(x∈(0,6])的图象总在函数y=f(x)图象的上方,则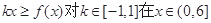 恒成立
分离参数得,
恒成立
分离参数得,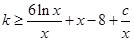 在
在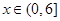 恒成立,又因为k∈[-1,1],所以
恒成立,又因为k∈[-1,1],所以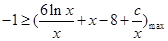
然后利用导数求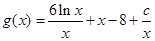 的最大值,再解不等式即可求得c的取值范围
的最大值,再解不等式即可求得c的取值范围
试题解析:(1)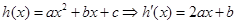
又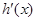 的图象过点(0,-8),(4,0),所以
的图象过点(0,-8),(4,0),所以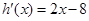 ,
,
于是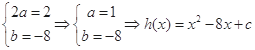 ,
,
故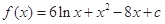 ,
,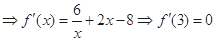
∴f(x)在点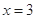 处的切线斜率为
处的切线斜率为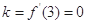 3分
3分
(2)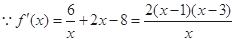 由
由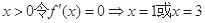 ,列表如下:
,列表如下:
|
x |
(0,1) |
1 |
(1, 3) |
3 |
(3,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
f(x) |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
所以f(x)的单调递增区间为(0,1)和(3,+∞),f(x)的单调递减区间为(1,3)
因为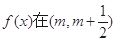 是单调函数,
是单调函数,
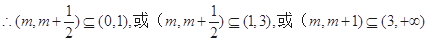
故实数m的取值范围为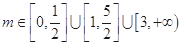 8分
8分
(3)由题意知: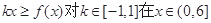 恒成立
恒成立
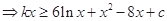 在
在 恒成立
恒成立
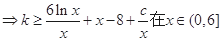 恒成立 9分
恒成立 9分
令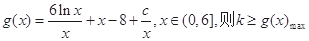

令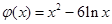 则
则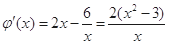
 内递减,
内递减,
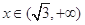 时,
时,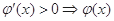 在
在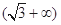 时
时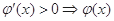 在
在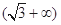 内递增,
内递增,
所以当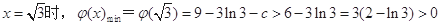
即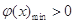 ,又
,又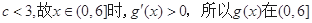 内递增
内递增
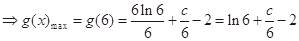 12分
12分
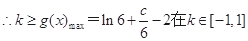 恒成立,
恒成立,
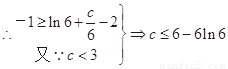 14分
14分
考点:导数与不等式

 名校课堂系列答案
名校课堂系列答案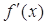
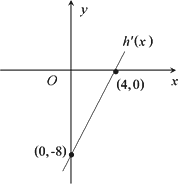
 的图象如图,f(x)=6lnx+h(x).
的图象如图,f(x)=6lnx+h(x).
 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;