题目内容
求函数解析式:
(1)已知一次函数f(x)满足f(0)=5,图象过点(-2,1),求f(x);
(2)已知二次函数g(x)满足g(1)=1,g(-1)=5,图象过原点,求g(x);
(3)已知二次函数h(x)与x轴的两交点为(-2,0),(3,0),且h(0)=-3,求h(x);
(4)已知二次函数F(x),其图象的顶点是(-1,2),且经过原点,求F(x).
答案:
解析:
提示:
解析:
|
解:(1)由题意设f(x)=ax+b,∵f(0)=5且图象过点(-2,1),∴ ∴f(x)=2x+5. (2)由题意设g(x)=ax2+bx+c,∵g(1)=1,g(-1)=5,且图象过原点,∴ ∴g(x)=3x2-2x. (3)由题意设h(x)=a(x+2)(x-3),又∵h(0)=-3,∴-6a=-3,得a= ∴h(x)= (4)由题意设F(x)=a(x+1)2+2,又∵图象经过原点,∴F(0)=0,∴a+2=0,得a=-2,∴F(x)=-2x2-4x. 点评:①已知函数类型,求函数解析式,常用待定系数法;②基本步骤:设出函数的一般式(或顶点式等),代入已知条件,通过解方程(组)确定未知系数. |
提示:
|
通过本题的训练,使学生加深对待定系数法的理解和运用. |

练习册系列答案
相关题目
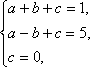 ∴
∴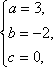
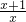 )=
)=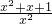 ,求f(x);
,求f(x); ,求f(x)、g(x);
,求f(x)、g(x);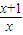 )=
)=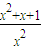 ,求f(x);
,求f(x);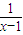 ,求f(x)、g(x);
,求f(x)、g(x);