题目内容
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数 的图象如图,f(x)=6lnx+h(x).
的图象如图,f(x)=6lnx+h(x).

①求f(x)在x=3处的切线斜率;
②若f(x)在区间(m,m+ )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;
③若对任意k∈[-1,1],函数y=kx(x∈(0,6])的图象总在函数y=f(x)图象的上方,求c的取值范围.
①0; ②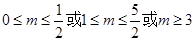 ;③
;③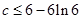
【解析】
试题分析:①根据图像求出一次导函数的解析式,那么函数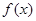 的导函数就很容易得到了,所求的切线斜率即是其所对应的的导函数值;②根据函数的单调性与导数的关系求出函数的三个单调区间,使得所给的区间在任何一个单调区间内即可求出未知数的取值范围;③由已知条件先导出和
的导函数就很容易得到了,所求的切线斜率即是其所对应的的导函数值;②根据函数的单调性与导数的关系求出函数的三个单调区间,使得所给的区间在任何一个单调区间内即可求出未知数的取值范围;③由已知条件先导出和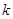 有关的不等式,将
有关的不等式,将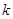 放在不等式的一边,那么就有
放在不等式的一边,那么就有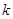 的最小值也要大于等于不等式另一边式子的最大值,才能保证不等式恒成立,由函数的单调性和导数的关系求最值即可.
的最小值也要大于等于不等式另一边式子的最大值,才能保证不等式恒成立,由函数的单调性和导数的关系求最值即可.
试题解析:①由已知得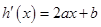 ,其图像如图所示过点
,其图像如图所示过点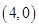 和
和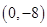 ,
,
则有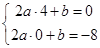 ,解得
,解得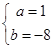 ,所以
,所以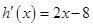 ,
,
所以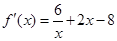 ,则
,则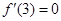 即
即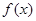 在
在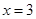 处的切线斜率为0;
3分
处的切线斜率为0;
3分
②由已知得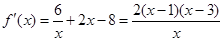
 ,
,
令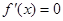 ,得
,得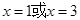 ,列表如下:
,列表如下:
|
x |
(0,1) |
1 |
(1, 3) |
3 |
(3,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
..f(x) |
|
极大值 |
|
极小值 |
|
要使f(x)在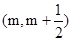 上是单调函数,则区间
上是单调函数,则区间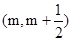 必须完全含在任意一个单调区间内, 5分
必须完全含在任意一个单调区间内, 5分
所以有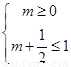 或
或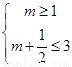 或
或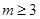 ,
,
所以m的取值范围为: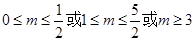 ;
7分
;
7分
③由题意知: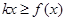 对
对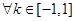 ,
,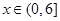 恒成立,
恒成立,
即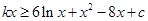 在
在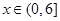 恒成立,
恒成立,
即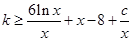 在
在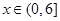 恒成立,
8分
恒成立,
8分
令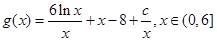 ,则
,则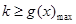 ,
,
因为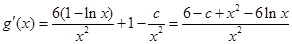 ,
,
令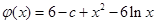 ,
, 则
则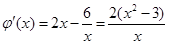 ,
,
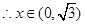 时,
时,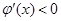 ,则
,则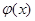 在
在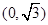 上是单调递减的,
上是单调递减的,
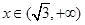 时,
时,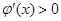 ,则
,则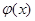 在
在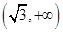 上是单调递增的,
上是单调递增的,
∴当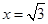 时,
时,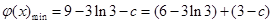 ,
,
又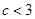 ,
,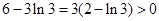 ,则
,则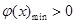 ,
,
所以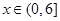 ,
,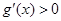 恒成立,则
恒成立,则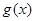 在
在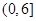 上是单调递增的,
上是单调递增的,
则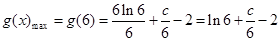 ,
.12分
,
.12分
 在
在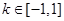 恒成立,
恒成立,
∴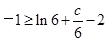 ,∴
,∴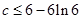 .
14分
.
14分
考点:函数的单调性和导数的关系,恒成立问题的解法.

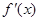
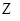
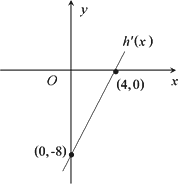
 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)
 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;