题目内容
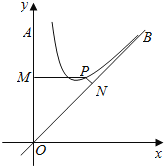
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 以
以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,设点
轴正半轴为极轴建立极坐标系,设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为正三角形.
为正三角形.
(1)求点![]() ,
,![]() 的极坐标;
的极坐标;
(2)若点![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最大值.
的最大值.
【答案】(1)![]()
![]() ,
,![]()
![]() ; (2)
; (2)![]() .
.
【解析】
(1)利用极坐标和直角坐标的互化公式,即得解;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,则点
,则点![]() 的直角坐标为
的直角坐标为![]() .将此代入曲线
.将此代入曲线![]() 的方程,可得点
的方程,可得点![]() 在以
在以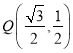 为圆心,
为圆心,![]() 为半径的圆上,所以
为半径的圆上,所以![]() 的最大值为
的最大值为![]() ,即得解.
,即得解.
(1)因为点![]() 在曲线
在曲线![]() 上,
上,![]() 为正三角形,
为正三角形,
所以点![]() 在曲线
在曲线![]() 上.
上.
又因为点![]() 在曲线
在曲线![]() 上,
上,
所以点![]() 的极坐标是
的极坐标是![]() ,
,
从而,点![]() 的极坐标是
的极坐标是![]() .
.
(2)由(1)可知,点![]() 的直角坐标为
的直角坐标为![]() ,B的直角坐标为
,B的直角坐标为![]()
设点![]() 的直角坐标为
的直角坐标为![]() ,则点
,则点![]() 的直角坐标为
的直角坐标为![]() .
.
将此代入曲线![]() 的方程,有
的方程,有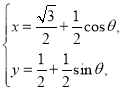
即点![]() 在以
在以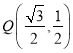 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】出版商为了解某科普书一个季度的销售量![]() (单位:千本)和利润
(单位:千本)和利润![]() (单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
(单位:元/本)之间的关系,对近年来几次调价之后的季销售量进行统计分析,得到如下的10组数据.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2.4 | 3.1 | 4.6 | 5.3 | 6.4 | 7.1 | 7.8 | 8.8 | 9.5 | 10 |
| 18.1 | 14.1 | 9.1 | 7.1 | 4.8 | 3.8 | 3.2 | 2.3 | 2.1 | 1.4 |
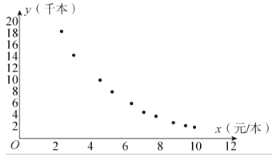
根据上述数据画出如图所示的散点图:
(1)根据图中所示的散点图判断![]() 和
和![]() 哪个更适宜作为销售量
哪个更适宜作为销售量![]() 关于利润
关于利润![]() 的回归方程类型?(给出判断即可,不需要说明理由)
的回归方程类型?(给出判断即可,不需要说明理由)
(2)根据(1)中的判断结果及参考数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)根据回归方程预测当每本书的利润为10.5元时的季销售量.
参考公式及参考数据:
①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的公式分别为
的斜率和截距的公式分别为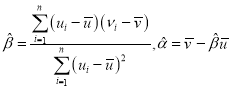 .
.
②参考数据:
|
|
|
|
|
|
|
6.50 | 6.60 | 1.75 | 82.50 | 2.70 |
|
|
表中![]() .另:
.另:![]() .计算时,所有的小数都精确到0.01.
.计算时,所有的小数都精确到0.01.
【题目】![]() 月份的二中迎来了国内外的众多宾客,其中很多人喜欢询问
月份的二中迎来了国内外的众多宾客,其中很多人喜欢询问![]() 团队模式,为了了解“询问
团队模式,为了了解“询问![]() 团队模式”是否与性别有关,在
团队模式”是否与性别有关,在![]() 月期间,随机抽取了
月期间,随机抽取了![]() 人,得到如下所示的列联表:
人,得到如下所示的列联表:
关心“ | 不关心“ | 合计 | |
男性 | 12 | ||
女性 | 36 | ||
合计 | 80 |
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,男性应抽
的样本,男性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为关心“
前提下,认为关心“![]() 团队”与性别有关系?
团队”与性别有关系?
(2)若以抽取样本的频率为概率,从![]() 月来宾中随机抽取
月来宾中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中关心“
人中关心“![]() 团队”人数为
团队”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
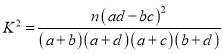
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |