题目内容
12.已知p:4x+1<0,q:x2-x-2>0,若p∨q为真,p∧q为假,求x的取值范围.分析 根据条件便知p,q中一真一假,通过解不等式可以得出p:x<−14,q:x<-1,或x>2,从而可求出p真q假和p假q真时x的范围再求并集即可得出x的取值范围.
解答 解:p∨q为真,p∧q为假;
∴p,q一真一假;
p:x<−14,q:x<-1,或x>2;
∴{x<−14−1≤x≤2,或{x≥−14x<−1,或x>2;
∴−1≤x<−14,或x>2;
∴x的取值范围为[-1,−14)∪(2,+∞).
点评 考查真、假命题的概念,p∨q,p∧q真假和p,q真假的关系,以及解一元二次不等式.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
20.已知α,β为锐角三角形的两个锐角,则以下结论正确的是( )
| A. | sinα<sinβ | B. | cosα<sinβ | C. | cosα<cosβ | D. | cosα>cosβ |
7.若集合A={x|-2<x<1},B={x|0<x<2},则集合A∩B=( )
| A. | { x|-1<x<1} | B. | { x|-2<x<1} | C. | { x|-2<x<2} | D. | { x|0<x<1} |
4.已知sinα=45,π2<α<π,那么tanα的值是( )
| A. | 43 | B. | -43 | C. | 34 | D. | -34 |
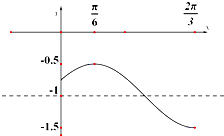 如果函数y=Asin(ωx+φ)+B(A>0,|φ|<
如果函数y=Asin(ωx+φ)+B(A>0,|φ|<