题目内容
如图，在平面直角坐标系xOy中， 点A为椭圆E：
（
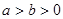）的左顶点， B，C在椭圆E上，若四边形OABC为平行四边形，且∠OAB＝30°，则椭圆E的离心率等于 .
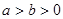（）的左顶点， B，C在椭圆E上，若四边形OABC为平行四边形，且∠OAB＝30°，则椭圆E的离心率等于 .
因为AO是与x轴重合的，且四边形OABC为平行四边形
所以BC∥OA，所以B、C两点的纵坐标相等，所以B、C的横坐标互为相反数.所以B、C两点是关于y轴对称的.由题知：OA=a,四边形OABC为平行四边形，所以BC=OA=a,
所以可设
,代入椭圆方程解得：
.
设D为椭圆的右顶点，因为∠OAB=30°，四边形OABC为平行四边形
所以∠COD=30°,对C点：
,解得：a=3b
根据：
所以BC∥OA，所以B、C两点的纵坐标相等，所以B、C的横坐标互为相反数.所以B、C两点是关于y轴对称的.由题知：OA=a,四边形OABC为平行四边形，所以BC=OA=a,
所以可设
,代入椭圆方程解得：.设D为椭圆的右顶点，因为∠OAB=30°，四边形OABC为平行四边形
所以∠COD=30°,对C点：
,解得：a=3b根据：
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
中，
，动点P的轨迹为曲线E，曲线E过点C且满足|PA|+|PB|为常数。
平分？若存在，求出L的斜率的取值范围；若不存在说明理由。
轴上，经过点
，离心率
．
、
，点
为直线
上任意一点（点
交椭圆于
点，连结
并延长交椭圆于
点，试问：是否存在
，使得
成立，若存在，求出
是椭圆
上的一点，若
，则点
斜率为
的直线过椭圆的上焦点且与椭圆相交于P，Q两点，线段PQ的垂直平分线与y轴交于点M(0，m)。
的焦点与椭圆
的焦点重合，则此双曲线的离心率为
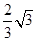
,点M(2,1).
，椭圆
以
的长轴为短轴，且与
，求直线
的方程
的离心率为
，长轴长为
，直线
交椭圆于不同的两点A、B.
的值（O点为坐标原点）；
的距离为
，求
面积的最大值.