Question

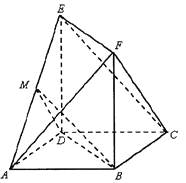
【题目】如图，四棱锥P-ABCD的底面ABCD为矩形，且PA=AD=1，AB=2，∠PAB=120°,∠PBC=90°.

（I）平面PAD与平面PAB是否垂直？并说明理由；

（II）求平面PCD与平面ABCD所成二面角的余弦值．

Answer 1

【答案】（I）平面 平面； （Ⅱ） cos∠PEF=.

【解析】

（１）说明，而，，即可说明平面PAD与平面PAB垂直；（2）以点A为坐标原点，AB所在的直线为ｙ轴建立空间直角坐标系，求出,,，进而求出, ，计算平面PCD的法向量为，平面ABCD的一个法向量为,代入夹角计算公式即可。

（I）平面 平面；

证明：由题意得且

又，则

则平面,

故平面平面

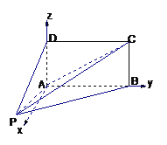
（Ⅱ）以点A为坐标原点，AB所在的直线为ｙ轴建立

空间直角坐标系如右图示，则,,

可得,

设平面PCD的法向量为,

则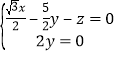， 令x=2得，

又平面ABCD的一个法向量为，

设平面PCD与平面ABCD所成二面角的大小为θ，显然为锐角θ，

∴cosθ==.

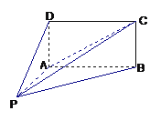
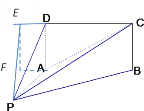
方法二：过点P作BA的垂线交BA的延长线于点F,过点F 作EF⊥AB,

交CD的延长线于点D.

则∠PEF为平面PCD与平面ABCD所成二面角的平面角

∵PA=1, ∠PAB=120°, ∴PF=,

又EF=AD=PA= 1，∴PE=,

∴cos∠PEF=.