题目内容
【题目】设函数f(x)=x3+bx2+cx(x∈R),已知g(x)=f(x)﹣f′(x)是奇函数
(1)求b、c的值.
(2)求g(x)的单调区间与极值.
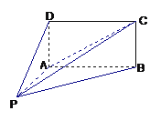
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)根据g(x)=f(x)﹣f'(x)是奇函数,且f'(x)=3x2+2bx+c能够求出b与c的值;
(2)对g(x)进行求导,g'(x)>0时的x的取值区间为单调递增区间,g'(x)<0时的x的取值区间为单调递减区间.g'(x)=0时的x函数g(x)取到极值.
(1)∵f(x)=x3+bx2+cx,∴f'(x)=3x2+2bx+c.
从而g(x)=f(x)﹣f'(x)=x3+bx2+cx﹣(3x2+2bx+c)=x3+(b﹣3)x2+(c﹣2b)x﹣c
是一个奇函数,所以g(0)=0得c=0,由奇函数定义得b=3;
(2)由(Ⅰ)知g(x)=x3﹣6x,从而g'(x)=3x2﹣6,
当g'(x)>0时,x<﹣![]() 或x>
或x>![]() ,
,
当g'(x)<0时,﹣![]() <x<
<x<![]() ,
,
由此可知,g(x)的单调递增区间为(﹣![]() ),(
),(![]() ,+∞);单调递减区间为(﹣
,+∞);单调递减区间为(﹣![]() ,
,![]() );
);
g(x)在x=﹣![]() 时取得极大值,极大值为4
时取得极大值,极大值为4![]() ,
,
g(x)在x=![]() 时取得极小值,极小值为4
时取得极小值,极小值为4![]() .
.

练习册系列答案
相关题目
【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |