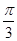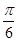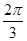题目内容
已知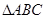 外接圆
外接圆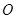 的半径为
的半径为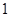 ,且
,且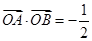 .
.
(Ⅰ)求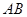 边的长及角
边的长及角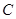 的大小;
的大小;
(Ⅱ)从圆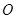 内随机取一个点
内随机取一个点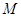 ,若点
,若点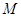 取自
取自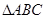 内的概率恰为
内的概率恰为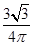 ,试判断
,试判断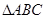 的形状.
的形状.
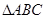 外接圆
外接圆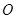 的半径为
的半径为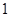 ,且
,且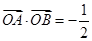 .
.(Ⅰ)求
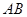 边的长及角
边的长及角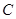 的大小;
的大小;(Ⅱ)从圆
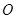 内随机取一个点
内随机取一个点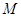 ,若点
,若点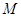 取自
取自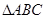 内的概率恰为
内的概率恰为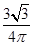 ,试判断
,试判断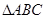 的形状.
的形状.(Ⅰ) ,
,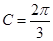 ;(Ⅱ)
;(Ⅱ)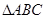 为等边三角形.
为等边三角形.
 ,
,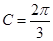 ;(Ⅱ)
;(Ⅱ)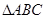 为等边三角形.
为等边三角形.试题分析:(Ⅰ)先利用
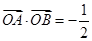 的定义结合
的定义结合 计算出
计算出 的大小,然后在
的大小,然后在 中利用余弦定理即可求出
中利用余弦定理即可求出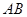 边的长,对于角
边的长,对于角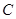 的大小可以根据性质“同弧所对的圆周角是圆心角的一半来计算;(Ⅱ)先利用几何概型计算出
的大小可以根据性质“同弧所对的圆周角是圆心角的一半来计算;(Ⅱ)先利用几何概型计算出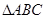 的面积,然后利用三角形的面积公式及余弦定理等求出
的面积,然后利用三角形的面积公式及余弦定理等求出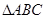 的三条边
的三条边 、
、 、
、 的大小,进而确定
的大小,进而确定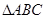 的形状.
的形状.试题解析:(Ⅰ)依题意
 , 2分
, 2分得
 ,又
,又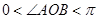 ,故
,故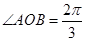 , 4分
, 4分又
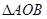 为等腰三角形, 故
为等腰三角形, 故 , 5分
, 5分而
 或
或 . 6分
. 6分(Ⅱ)依题意,从圆
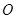 内随机取一个点,取自
内随机取一个点,取自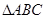 内的概率
内的概率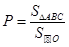 ,
,可得
 . 8分
. 8分设
 ,
, .设
.设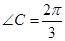 ,由
,由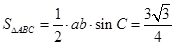 ,得
,得 , ①
, ① 由
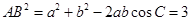 ,得
,得 , ②
, ②联立①②得
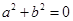 ,这是不可能的. 所以必有
,这是不可能的. 所以必有 . 9分
. 9分由
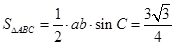 ,得
,得 , ①
, ①由
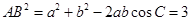 ,得
,得 ,
,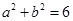 ② 11分
② 11分联立①② 解得
 .
.所以
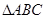 为等边三角形. 12分
为等边三角形. 12分
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,函数
,函数 .
. 的最值和单调递减区间;
的最值和单调递减区间; ,
, ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.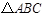 中,若
中,若 ,则
,则 = .
= . ,c=
,c= +1,求A
+1,求A 中,角
中,角 的对边分别是
的对边分别是 ,且
,且
 的大小:
的大小:  ,且
,且 ,求
,求 中,下列关系式不一定成立的是( )。
中,下列关系式不一定成立的是( )。



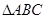 中,角
中,角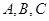 所对边长分别为
所对边长分别为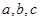 ,若
,若 ,则
,则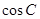 的最小值为( )
的最小值为( )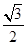
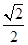
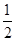
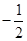
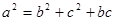 ,则角A为( )
,则角A为( )