题目内容
11.数列{an},a1=1,an+1=$\sqrt{{a}_{n}^{2}-2{a}_{n}+2}$-1(n∈N*),问:是否存在实数t,对?n∈N*恒有a2n<t<a2n+1,若存在,求出t;若不存在,讲理由.分析 通过记f(x)=$\sqrt{(x-1)^{2}+1}$-1,并令t=f(t)可知t=$\frac{1}{4}$,从而a2n<$\frac{1}{4}$<a2n+1,用数学归纳法证明即可.
解答 结论:存在实数t=$\frac{1}{4}$,对?n∈N*恒有a2n<t<a2n+1.
理由如下:
an+1=$\sqrt{{a}_{n}^{2}-2{a}_{n}+2}$-1=$\sqrt{({a}_{n}-1)^{2}+1}$-1(n∈N*),
记f(x)=$\sqrt{(x-1)^{2}+1}$-1,
令t=f(t),解得:t=$\frac{1}{4}$,
下面用数学归纳法证明:a2n<$\frac{1}{4}$<a2n+1.
①当n=1时,a2=f(a1)=f(1)=0,
a3=f(a2)=f(0)=$\sqrt{2}$-1,
显然a2<$\frac{1}{4}$<a3;
②假设当n=k(k≥2)时,有a2k<$\frac{1}{4}$<a2k+1,
∵f(x)=$\sqrt{(x-1)^{2}+1}$-1在区间(-∞,1]上单调递减,
∴t=f(t)>f(a2k+1)=a2k+2,
∴t=f(t)<f(a2k+2)=a2k+3,
即a2(k+1)<t<a2(k+1)+1,
∴当n=k+1时,命题也成立;
由①、②可知:a2n<$\frac{1}{4}$<a2n+1.
点评 本题考查数列递推式、数列的通项,考查数学归纳法,考查学生分析解决问题的能力,注意解题方法的积累,属于难题.

练习册系列答案
相关题目
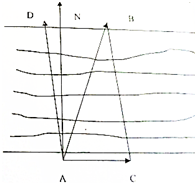 在长江某流口处,江水以5km/h的速度向东流,一渡船在江南岸的A码头,预定要在0.1h后到达北岸B码头,如图,设$\overrightarrow{AN}$为正北方向,已知B码头在A码头的北偏东15°,并与A码头相距1.2km,该渡船应按什么方向航行?速度是多少?(角度精确到0.1°,速度精确到0.1km/h)
在长江某流口处,江水以5km/h的速度向东流,一渡船在江南岸的A码头,预定要在0.1h后到达北岸B码头,如图,设$\overrightarrow{AN}$为正北方向,已知B码头在A码头的北偏东15°,并与A码头相距1.2km,该渡船应按什么方向航行?速度是多少?(角度精确到0.1°,速度精确到0.1km/h)