题目内容
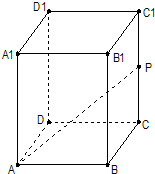 (2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)
(2012•长宁区一模)在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD的边长为2,点P是CC1的中点,直线AP与平面BCC1B1成30°角,求异面直线BC1和AP所成角的大小.(结果用反三角函数值表示)分析:欲求异面直线BC1和AP所成角,先平移其中一条直线,使其成为相交直线,则相交直线所成角即为异面直线所成角,本题中,容易判断AD1∥BC1,所以∠D1AP是异面直线BC1和AP所成的角.再放入△D1AP中,用余弦定理来求即可.
解答: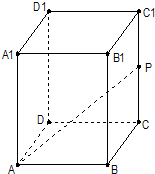 解:连接BP,设长方体的高为h,
解:连接BP,设长方体的高为h,
因为AB⊥平面BCC1B1,
所以,∠APB即为直线AP与平面BCC1B1所成的角
PB=
,
由tan600=
得h=4
.
又因为AD1∥BC1,
所以∠D1AP是异面直线BC1和AP所成的角.
在△D1AP中,AD1=6,PA=4,D1P=2
,
所以,cos∠D1AP=
=
,即∠D1AP=arccos
 解:连接BP,设长方体的高为h,
解:连接BP,设长方体的高为h,因为AB⊥平面BCC1B1,
所以,∠APB即为直线AP与平面BCC1B1所成的角
PB=
|
由tan600=
| ||||
| 2 |
| 2 |
又因为AD1∥BC1,
所以∠D1AP是异面直线BC1和AP所成的角.
在△D1AP中,AD1=6,PA=4,D1P=2
| 3 |
所以,cos∠D1AP=
| 16+36-12 |
| 2•4•6 |
| 5 |
| 6 |
| 5 |
| 6 |
点评:本题主要考查了异面直线所成角的求法,关键是如何把异面直线所成角转化为平面角.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目