题目内容
20.已知函数f(x)=acosx+b的最小值是-$\frac{1}{2}$,最大值是$\frac{3}{2}$,求a,b的值.分析 根据余弦函数的有界性,讨论a的取值范围,结合函数y的最大、最小值,列出方程组,求出a,b的值.
解答 解:∵-1≤cosx≤1,
∴当a>0时,-a≤acosx≤a,
∴-a+b≤acosx+b≤a+b;
由函数y=acosx+b的最小值是-$\frac{1}{2}$,最大值是$\frac{3}{2}$,
得$\left\{\begin{array}{l}b-a=-\frac{1}{2}\\ b+a=\frac{3}{2}\end{array}\right.$,
解得a=1,b=$\frac{1}{2}$;
当a=0时,不满足题意;
当a<0时,a≤acosx≤-a,
∴a+b≤acosx+b≤-a+b,
由函数y=acosx+b的最大值为1,最小值为-7,
得$\left\{\begin{array}{l}b-a=\frac{3}{2}\\ b+a=-\frac{1}{2}\end{array}\right.$,
解得a=-1,b=$\frac{1}{2}$;
综上,a=1,b=$\frac{1}{2}$,或a=-1,b=$\frac{1}{2}$.
点评 本题考查了三角函数的最值问题,也考查了方程组的解法与应用问题以及分类讨论思想的应用问题,是基础题目.

练习册系列答案
相关题目
11.设a>1,b>1且ab-(a+b)=1,那么( )
| A. | ab有最大值$2\sqrt{2}+1$ | B. | ab有最小值${(\sqrt{2}+2)^2}$ | C. | ab有最小值${(\sqrt{2}+1)^2}$ | D. | ab有最大值$2(\sqrt{2}+1)$ |
15.命题“?x∈[-1,2],x2-2x-a≤0”为真命题,则实数a的取值范围是( )
| A. | a≥3 | B. | a≤3 | C. | a≥0 | D. | a≤0 |
5.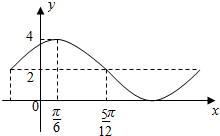 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,||φ|<$\frac{π}{2}$,则( )| A. | B=1 | B. | φ=$\frac{π}{6}$ | C. | ω=1 | D. | A=4 |
10.已知a>1,若函数f(x)=logax-ax有零点,则a的取值范围是( )
| A. | (1,e] | B. | (1,$\sqrt{e}$] | C. | (1,${e}^{\frac{1}{e}}$] | D. | (1,${e}^{\sqrt{e}-1}$] |