题目内容
15.命题“?x∈[-1,2],x2-2x-a≤0”为真命题,则实数a的取值范围是( )| A. | a≥3 | B. | a≤3 | C. | a≥0 | D. | a≤0 |
分析 问题掌握即a≥(x-1)2-1,求出y=(x-1)2-1的单调区间,从而求出函数的最大值即可.
解答 解:x∈[-1,2],x2-2x-a≤0,即a≥(x-1)2-1,
y=(x-1)2-1的对称轴是x=1,
函数在[-1,1)递减,在(1,2]递增,
∴x=-1时函数取得最大值,函数的最大值是3,
“?x∈[-2,1],使x2+2x+a≥0”为真命题,
∴a≥3,
故选:A.
点评 本题考查了求函数恒成立问题,考查转化思想,是一道基础题.

练习册系列答案
相关题目
3.$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$能构成空间的-个基底的条件是( )
| A. | O,A,B,C四点任意三点不共线 | B. | O,A,B,C四点不共面 | ||
| C. | A,B,C三点共线 | D. | 存在实数x,y,z,使x $\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$=$\overrightarrow{0}$ |
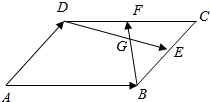 如图所示,?ABCD中,E、F分别是BC、DC的中点,BF与DE交于点G,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,?ABCD中,E、F分别是BC、DC的中点,BF与DE交于点G,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.