题目内容
8. 图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2
图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2(Ⅰ)求证:AC∥平面PBE
(Ⅱ)求平面PBE与平面PAD夹角的余弦值.
分析 (Ⅰ)连接AC,与BD相交于O,取PB的中点H,连接HE,HO,证明四边形OCEH是平行四边形,可得OC∥HE,即可证明AC∥平面PBE
(Ⅱ)建立如图所示的坐标系,求出平面PAD的法向量、平面PBE的法向量,即可求平面PBE与平面PAD夹角的余弦值.
解答 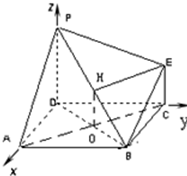 (Ⅰ)证明:连接AC,与BD相交于O,取PB的中点H,连接HE,HO,
(Ⅰ)证明:连接AC,与BD相交于O,取PB的中点H,连接HE,HO,
∵HO是△BDP的中位线,
∴OH∥PD,OH=$\frac{1}{2}$PD,
∵CE∥PD,CE=$\frac{1}{2}$PD,
∴OH∥CE,OH=CE,
∴四边形OCEH是平行四边形,
∴OC∥HE,
∵HE?平面PBE,OC?平面PBE,
∴AC∥平面PBE;
(Ⅱ)解:建立如图所示的坐标系,则D(0,0,0),C(0,2,0),B(2,2,0),P(0,0,2),E(0,2,1),
∴$\overrightarrow{DC}$=(0,2,0)是平面PAD的法向量,
设平面PBE的法向量为$\overrightarrow{n}$=(x,y,z),则
∵$\overrightarrow{BP}$=(-2,-2,2),$\overrightarrow{BE}$=(-2,0,1),
∴$\left\{\begin{array}{l}{-2x-2y+2z=0}\\{-2x+z=0}\end{array}\right.$,
取z=1,则$\overrightarrow{n}$=($\frac{1}{2}$,$\frac{1}{2}$,1),
∴平面PBE与平面PAD夹角的余弦值|$\frac{1}{2×\frac{\sqrt{6}}{2}}$|=$\frac{\sqrt{6}}{6}$
点评 本题考查线面平行的判定,考查平面PBE与平面PAD夹角的余弦值,正确证明四边形OCEH是平行四边形、求出平面的法向量是关键.

| A. | (3,+∞) | B. | (1,3) | C. | (-∞,3) | D. | (-∞,3] |
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
本题可以参考独立性检验临界值表
| P(K2≥k) | 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.535 | 7.879 | 10. 828 |

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
 定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )
定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )