题目内容
（2013•重庆）已知函数f（x）=ax3+bsinx+4（a，b∈R），f（lg（log210））=5，则f（lg（lg2））=（ ）
| A．﹣5 | B．﹣1 | C．3 | D．4 |
C
∵lg（log210）+lg（lg2）=lg1=0，
∴lg（log210）与lg（lg2）互为相反数
则设lg（log210）=m，那么lg（lg2）=﹣m
令f（x）=g（x）+4，即g（x）=ax3+bsinx，此函数是一个奇函数，故g（﹣m）=﹣g（m），
∴f（m）=g（m）+4=5，g（m）=1
∴f（﹣m）=g（﹣m）+4=﹣g（m）+4=3．
故选C．
∴lg（log210）与lg（lg2）互为相反数
则设lg（log210）=m，那么lg（lg2）=﹣m
令f（x）=g（x）+4，即g（x）=ax3+bsinx，此函数是一个奇函数，故g（﹣m）=﹣g（m），
∴f（m）=g（m）+4=5，g（m）=1
∴f（﹣m）=g（﹣m）+4=﹣g（m）+4=3．
故选C．
练习册系列答案
阅读快车系列答案
相关题目
(－x2＋6x)的值域( )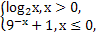
则f(f(1))+f
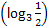的值是__________.
中，下列描述正确的是（ ）
、值域是R ②图像必过点(1,0).
时，在
时，在
，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求
的最小值．
的定义域是 ．