题目内容
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
(1)求k的值;
(2)设g(x)=log4
 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.(1)k=-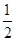 .(2){-3}∪(1,+∞).
.(2){-3}∪(1,+∞).
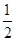 .(2){-3}∪(1,+∞).
.(2){-3}∪(1,+∞).(1)由函数f(x)是偶函数,可知f(x)=f(-x),
∴log4(4x+1)+kx=log4(4-x+1)-kx.
log4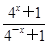 =-2kx,即x=-2kx对一切x∈R恒成立,∴k=-
=-2kx,即x=-2kx对一切x∈R恒成立,∴k=-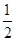 .
.
(2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log4(4x+1)-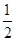 x=log4
x=log4 有且只有一个实根,化简得方程2x+
有且只有一个实根,化简得方程2x+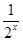 =a·2x-
=a·2x-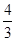 a有且只有一个实根.令t=2x>0,则方程(a-1)t2-
a有且只有一个实根.令t=2x>0,则方程(a-1)t2-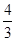 at-1=0有且只有一个正根.
at-1=0有且只有一个正根.
①a=1?t=-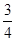 ,不合题意;②a≠1时,Δ=0?a=
,不合题意;②a≠1时,Δ=0?a=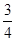 或-3.若a=
或-3.若a=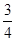 ?t=-2,不合题意,若a=-3?t=
?t=-2,不合题意,若a=-3?t=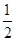 ;③a≠1时,Δ>0,一个正根与一个负根,即
;③a≠1时,Δ>0,一个正根与一个负根,即 <0?a>1.
<0?a>1.
综上,实数a的取值范围是{-3}∪(1,+∞).
∴log4(4x+1)+kx=log4(4-x+1)-kx.
log4
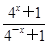 =-2kx,即x=-2kx对一切x∈R恒成立,∴k=-
=-2kx,即x=-2kx对一切x∈R恒成立,∴k=-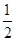 .
.(2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log4(4x+1)-
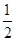 x=log4
x=log4 有且只有一个实根,化简得方程2x+
有且只有一个实根,化简得方程2x+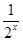 =a·2x-
=a·2x-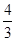 a有且只有一个实根.令t=2x>0,则方程(a-1)t2-
a有且只有一个实根.令t=2x>0,则方程(a-1)t2-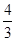 at-1=0有且只有一个正根.
at-1=0有且只有一个正根.①a=1?t=-
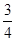 ,不合题意;②a≠1时,Δ=0?a=
,不合题意;②a≠1时,Δ=0?a=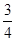 或-3.若a=
或-3.若a=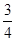 ?t=-2,不合题意,若a=-3?t=
?t=-2,不合题意,若a=-3?t=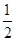 ;③a≠1时,Δ>0,一个正根与一个负根,即
;③a≠1时,Δ>0,一个正根与一个负根,即 <0?a>1.
<0?a>1.综上,实数a的取值范围是{-3}∪(1,+∞).

练习册系列答案
相关题目
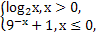 则f(f(1))+f
则f(f(1))+f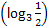 的值是__________.
的值是__________. ,
, 的值域是 .
的值域是 . ,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求
,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求 的最小值.
的最小值.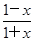 是________(填“奇”或“偶”)函数.
是________(填“奇”或“偶”)函数.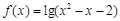 ,x∈R},B={x||x-i|<
,x∈R},B={x||x-i|<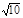 ,i为虚数单位,x>0},则A
,i为虚数单位,x>0},则A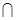 B=( )
B=( ) 的定义域是
的定义域是


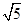 +lg
+lg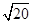 =________.
=________.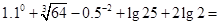 .
.