题目内容
在平面直角坐标系xOy中,点P是圆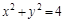 上一动点,
上一动点,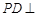 x轴于点D.记满足
x轴于点D.记满足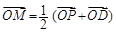 的动点M的轨迹为Γ.
的动点M的轨迹为Γ.
(1)求轨迹Γ的方程;
(2)已知直线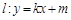 与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且
与轨迹Γ交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且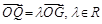 .
.
①证明: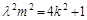
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
(1)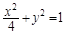 ;(2)
;(2)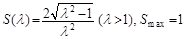
解析试题分析:(1)由已知M是PD的中点,利用P点在圆上,可以求出M的点轨迹方程为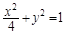 ;(2)点Q在(1)中的椭圆上,G是OQ上的分点,利用直线与椭圆的关系,可以找到λ与m和k的关系,并进一步将三角形AOB的面积表示成λ的函数关系式,再求出它的最大值.
;(2)点Q在(1)中的椭圆上,G是OQ上的分点,利用直线与椭圆的关系,可以找到λ与m和k的关系,并进一步将三角形AOB的面积表示成λ的函数关系式,再求出它的最大值.
试题解析:(1)设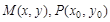 ,则点
,则点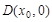 ,且
,且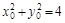 (1)
(1)
∵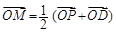
∴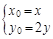 (2)
(2)
将(2)代入(1),得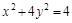
∴轨迹Γ的方程为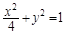 ; 5分
; 5分
(2)①令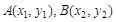
由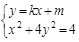 消去y
消去y
得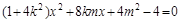 6分
6分
∴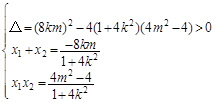 ,即
,即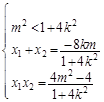 (3)
(3)
∴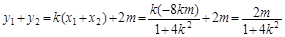
又由中点坐标公式,得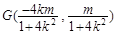
根据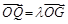 ,得
,得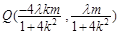
将其代入椭圆方程,有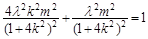
化简得: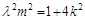 (4) 9分
(4) 9分
②由(3)(4)得
∵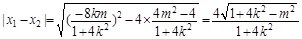 (5)
(5)
在△AOB中,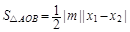 (6)
(6)
∴由(4)(5)(6)可得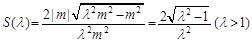 12分
12分
令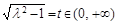
则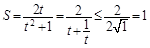 (当且仅当t=1时,即
(当且仅当t=1时,即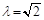 时取“=”)
时取“=”)
∴当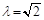 时,
时,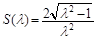 取得最大值,其最大值为1. 13分
取得最大值,其最大值为1. 13分
考点:动点轨迹,直线与椭圆的位置关系,中点坐标,平面向量的坐标运算,基本不等式,范围与最值.

练习册系列答案
相关题目
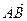 |=2|
|=2|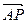 |,则点P的坐标为____________.
|,则点P的坐标为____________. 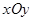 中,已知点
中,已知点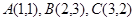 ,点
,点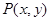 在
在 三边围成的区域(含边界)上
三边围成的区域(含边界)上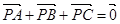 ,求
,求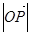 ;
;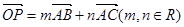 ,用
,用 表示
表示 ,并求
,并求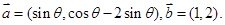
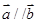 ,求
,求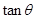 的值;
的值;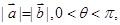 求
求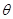 的值。
的值。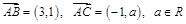
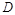 为
为 的中点,
的中点,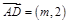 ,求
,求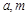 的值;
的值;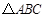 是以
是以 为斜边的直角三角形,求
为斜边的直角三角形,求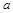 的值.
的值.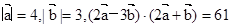 ,
,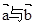 的夹角
的夹角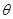 ; (2)求
; (2)求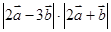 的值.
的值.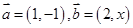 ,若
,若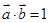 ,则
,则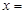 _______________.
_______________.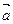 =(2,-1),向量
=(2,-1),向量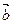 与
与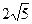 ,则
,则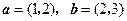 ,若向量
,若向量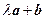 与向量
与向量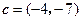 共线,则
共线,则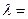 。
。