题目内容
7.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC为球O的直径,且SC⊥OA,SC⊥OB,△OAB为等边三角形,三棱锥S-ABC的体积为$\frac{{4\sqrt{3}}}{3}$,则球O的表面积是16π.分析 根据题意作出图形.三棱锥S-ABC的体积可看成是两个三棱锥S-ABO和C-ABO的体积和,求出球的半径,即可求出球O的表面积.
解答 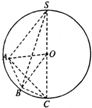 解:根据题意作出图形.设球心为O,球的半径为r.
解:根据题意作出图形.设球心为O,球的半径为r.
∵SC⊥OA,SC⊥OB,∴SC⊥平面AOB.
三棱锥S-ABC的体积可看成是两个三棱锥S-ABO和C-ABO的体积和.
∴V三棱锥S-ABC=V三棱锥S-ABO+V三棱锥C-ABO
=$\frac{1}{3}×\frac{{\sqrt{3}}}{4}×{r^2}×r×2=\frac{{4\sqrt{3}}}{3},\;∴r=2$.
∴球的表面积是S=16π.
故答案为:16π.
点评 本题考查球O的表面积,考查三棱锥S-ABC的体积,确定球的半径是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.执行如图所示的程序框图,若a=9,b=1,则输出的结果是( )


| A. | 9 | B. | 11 | C. | 13 | D. | 15 |
18.执行如图所示的程序框图,输入m=1173,n=828,则输出的实数m的值是( )


| A. | 68 | B. | 69 | C. | 138 | D. | 139 |
15.已知集合M={x|x2-1≤0},N={x|$\frac{1}{2}$<2x+1<4,x∈Z},则M∩N=( )
| A. | {-1,0} | B. | {1} | C. | {-1,0,1} | D. | ∅ |
12.下列有关命题的说法正确的是( )
| A. | “x=6”是“x2-5x-6=0”的必要不充分条件 | |
| B. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| C. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| D. | 命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,均有x2+x+1>0” |
2.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是棱AA1,DD1的中点,则直线EF被该正方体的外接球所截得的线段长为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
19.随机抽查部分成人,得到吸烟与性别的情况如下:
以下哪个值越大,则表明性别与吸烟之间有关系的可能性越大?( )
| 吸烟 | 不吸烟 | |
| 男士 | a | c |
| 女士 | b | d |
| A. | ad-bc | B. | ac-bd | C. | |ad-bc| | D. | |ac-bd| |