题目内容
10．画出不等式（x+2y+1）（x-y-4）＜0表示的平面区域．分析 将不等式进行转化，可得两组不等式组，进行线性规划，可得答案．
解答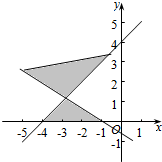 
解：不等式（x+2y+1）（x-y-4）＜0，
可转化为$\left\{\begin{array}{l}{x+2y+1＞0}\\{x-y+4＜0}\end{array}\right.$或$\left\{\begin{array}{l}{x+2y+1＜0}\\{x-y+4＞0}\end{array}\right.$，
作出图象，如图所示．
点评 此题考查了二元一次不等式（组）与平面区域，
练习册系列答案
相关题目
2．
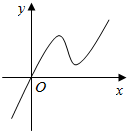已知函数f（x）的定义域为R，且满足f（4）=1，f′（x）为f（x）的导函数，又知y=f′（x）的图象如图所示，若两个正数a，b满足，f（2a+b）＜1，则$\frac{b+2}{a+1}$的取值范围是（ ）
已知函数f（x）的定义域为R，且满足f（4）=1，f′（x）为f（x）的导函数，又知y=f′（x）的图象如图所示，若两个正数a，b满足，f（2a+b）＜1，则$\frac{b+2}{a+1}$的取值范围是（ ）| A． | $（{\frac{2}{3}，6}）$ | B． | $[{\frac{2}{3}，6}]$ | C． | $[\frac{1}{4}，\frac{5}{2}]$ | D． | $（{\frac{1}{4}，\frac{5}{2}}）$ |
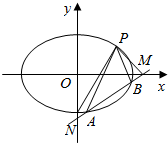如图，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$，过椭圆C上一点P（2，1）作倾斜角互补的两条直线，分别与椭圆交于点A、B，直线AB与x轴交于点M，与y轴负半轴交于点N．