题目内容
【题目】设f(x)=log3x.
(1)若![]() ,判断并证明函数y=g(x)的奇偶性;
,判断并证明函数y=g(x)的奇偶性;
(2)令![]() ,x∈[3,27],当x取何值时h(x)取得最小值,最小值为多少?
,x∈[3,27],当x取何值时h(x)取得最小值,最小值为多少?
【答案】(1)奇函数(2)当x=3时h(x)取得最小值,最小值为1
【解析】
试题分析:(1)根据对数函数的性质,先求出定义域,再根据奇偶性的定义即可判断;(2)先化简h(x),再t=log3x,3≤x≤27,则1≤t≤3根据二次函数的性质即可求出
试题解析:(1)![]() ,
,
∴![]() 的定义域为(﹣∞,﹣1)∪(1,+∞),
的定义域为(﹣∞,﹣1)∪(1,+∞),
![]() =
=![]()
∴函数y=g(x)为奇函数.
(2)∵![]() ,3≤x≤27
,3≤x≤27
设t=log3x,3≤x≤27,∴1≤t≤3
令![]() ,1≤t≤3
,1≤t≤3
当t=1时,即x=3时,ymin=1
∴当x=3时h(x)取得最小值,最小值为1.

练习册系列答案
相关题目
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
分数区间 | 甲班频率 | 乙班频率 |
| 0.1 | 0.2 |
| 0.2 | 0.2 |
| 0.3 | 0.3 |
| 0.2 | 0.2 |
| 0.2 | 0.1 |
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的![]() ×
×![]() 列联表:
列联表:
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
参考公式: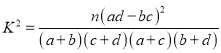 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|