题目内容
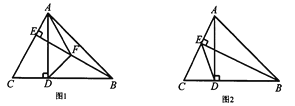
【题目】如图,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,E,F分别为
,E,F分别为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使得
折起,使得![]() .
.
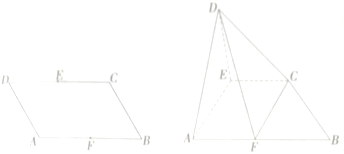
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证平面![]() 平面
平面![]() ,只要证
,只要证![]() 面
面![]() 即可,由已知有
即可,由已知有![]() ,
,![]() ,
,![]() ,可证
,可证![]() 面
面![]() ;
;
(2)作![]() ,由已知可证
,由已知可证![]() 为为二面角的平面角,在三角形
为为二面角的平面角,在三角形![]() 中计算各边的长度,由余弦定理求之即可;或由已知,
中计算各边的长度,由余弦定理求之即可;或由已知,![]() ,
,![]() ,
,![]() ,过点E 作
,过点E 作![]() 轴
轴![]() 面ABCE,建立如图所示空间直角坐标系,用空间向量求之即可.
面ABCE,建立如图所示空间直角坐标系,用空间向量求之即可.
试题解析:
(1)证明:由已知![]() ,
,![]() ,
,![]() ,
,
![]() 面
面![]() ,
,
又![]() CF,
CF, ![]() 面
面![]() , img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/09/3091cb5b/SYS201712290946535124467089_DA/SYS201712290946535124467089_DA.019.png" width="42" height="20" style="-aw-left-pos:0pt; -aw-rel-hpos:page; -aw-rel-vpos:page; -aw-top-pos:0pt; -aw-wrap-type:inline" />面DCF,
, img src="http://thumb.zyjl.cn/questionBank/Upload/2017/12/29/09/3091cb5b/SYS201712290946535124467089_DA/SYS201712290946535124467089_DA.019.png" width="42" height="20" style="-aw-left-pos:0pt; -aw-rel-hpos:page; -aw-rel-vpos:page; -aw-top-pos:0pt; -aw-wrap-type:inline" />面DCF,
![]() 平面
平面![]() 平面
平面![]() .
.
(2)方法①![]() 面
面![]() ,作
,作![]() ,则
,则![]() ,
,
![]() 即为所求二面角的平面角
即为所求二面角的平面角
![]() ,
,![]() ,
,![]() ,
,![]() 9分
9分
在![]() 中,
中,![]() ,
,
![]() 1
1
方法②由已知,![]() ,
,![]() ,
,![]() ,过点E 作
,过点E 作![]() 轴
轴![]() 面ABCE,
面ABCE,
如图,建立空间直角坐标系.
![]()
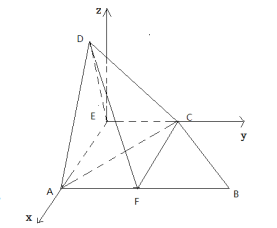
可得:E(0,0,0),A(![]() ,0,0),
,0,0),
C(0,1,0) ,D(![]() )
)
![]() ,
,![]() ,设平面DCA的法向量为
,设平面DCA的法向量为![]() ,
,
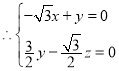 解得:
解得:![]() ,
,
又平面DCE的法向量为![]() ,
,![]() ,
,
![]() 二面角E-DC-A的余弦值
二面角E-DC-A的余弦值![]() 1
1

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目