��Ŀ����
5�����壺��Բ�IJ�ͬ����Բ����C1����x-a1��2+��y-b1��2=r12��C2����x-a2��2+��y-b2��2=r22���߷ֱ�������õ�ֱ��m��Ϊ��Բ�ĸ��ᣮ��1����֤�������ᡱ����ֱ��m����ԲԲ�ĵ����ߴ�ֱ��
��2����֤�������ᡱ����ֱ��m����Բ�ⲿ�ֵĵ㵽��Բ�����߳���ȣ�
��3���������������жϣ�����ԲC��x2+y2-2x+4y-4=0��˵���Ƿ����б��Ϊ1��ֱ��l��ʹ��l��ԲC�صõ���ABΪֱ����Բ������ԭ�㣿�����ڣ�д��ֱ��l�ķ��̣��������ڣ�˵�����ɣ�
���� ��1�����������á����ᡱ�Ķ��壬����Բ�ĺ����ҵ��е�����ߴ�ֱ��ƽ���ң��ɵá����ᡱ����ֱ��m����ԲԲ�ĵ����ߴ�ֱ��
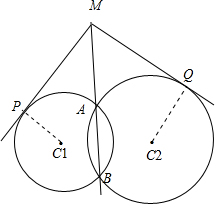
��2��֤�������M�ǣ������ᡱ����ֱ��m����Բ�ⲿ�ֵĵ㣬��ͼ��ʾ��MP��MQ�ֱ�Ϊ��Բ�����߳��������и��߶����ɵ�MP=MQ��
��3���������ֱ��l��y=x+b����������Բ�ķ��̿ɵ�2x2+��2b+2��b2+4b-4=0 �٣���A��x1��y1����B�� x2��y2��������Τ�ﶨ�����Լ�OA��OB���ɵ� x1•x2+y1•y2=0�����b=1����b=-4���ٰ�b=1����b=-4����ټ��飬�б�ʽ�������㣬�ɵ�����������ֱ����������
���  �⣺��1��֤����������ɵá����ᡱ����Բ�Ĺ��������ڵ�ֱ�ߣ��ٸ�����Բ�ཻ�����ʿɵã�
�⣺��1��֤����������ɵá����ᡱ����Բ�Ĺ��������ڵ�ֱ�ߣ��ٸ�����Բ�ཻ�����ʿɵã�
Բ�ĺ����ҵ��е�����ߴ�ֱ��ƽ���ң�
�ʡ����ᡱ����ֱ��m����ԲԲ�ĵ����ߴ�ֱ��
��2��֤�������M�ǣ������ᡱ����ֱ��m����Բ�ⲿ�ֵĵ㣬��ͼ��ʾ��MP��MQ�ֱ�Ϊ��Բ�����߳���
�����и��߶����ɵ�MA•MB=MP2��MA•MB=MQ2����MP=MQ��
�������ᡱ����ֱ��m����Բ�ⲿ�ֵĵ㵽��Բ�����߳���ȣ�
��3���������ֱ��l��y=x+b������$\left\{\begin{array}{l}{{x}^{2}{+y}^{2}-2x+4y-4=0}\\{y=x+b}\end{array}\right.$���ɵ�2x2+��2b+2��b2+4b-4=0 �٣�
��A��x1��y1����B�� x2��y2������x1+x2=-b-1��x1•x2=$\frac{{b}^{2}+2b-4}{2}$��
��y1•y2=��x1+b����x2+b��=x1•x2+b��x1+x2��+b2=$\frac{{b}^{2}+4b-4}{2}$+b��-b-1��+b2=$\frac{{b}^{2}+2b-4}{2}$��
��OA��OB����x1•x2+y1•y2=0���� $\frac{{b}^{2}+4b-4}{2}$+$\frac{{b}^{2}+2b-4}{2}$=0�����b=1����b=-4��
�ٰ�b=1����b=-4����ټ��飬�б�ʽ�������㣬������������ֱ������������ x-y+1=0 x-y-4=0��
���� ������Ҫ�����¶��壬Բ���и��߶�����ֱ�ߺ�Բ�ཻ�����ʣ������е��⣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | A��B����� | B�� | A��B�������� | C�� | P��A+B��=P��A��+P��B�� | D�� | B?A |