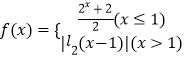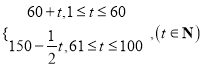Question

【题目】已知函数 ，
（1）若 ，求 的最大值；
（2）若 恒成立，求实数 的取值范围。

Answer 1

【答案】
（1）解： ，

.

则 ， ，

， ， 在 上为增函数，

（2）解： ，即 对 恒成立，

.

设 ，则 ，

， 在 上递减，

，

【解析】(1)利用导数的定义得到f′(1)=2=a+1求出a的值，然后利用导数的性质求出函数的增减性进而求出最值。(2)由恒成立问题，利用变量分离转化求出最值。
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减；求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．