ЬтФПФкШн
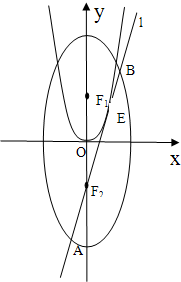 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
ЃЈ1ЃЉЧѓжЄЃКЧаЯпlЕФаБТЪЮЊЖЈжЕЃЛ
ЃЈ2ЃЉШєЖЏЕуTТњзуЃК
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
| ET |
| OT |
| 5 |
| 4 |
ЃЈ3ЃЉЕБІЫЁЪ[2ЃЌ4]ЪБЃЌЧѓЭждВРыаФТЪeЕФШЁжЕЗЖЮЇЃЎ
ЗжЮіЃКЃЈ1ЃЉгЩЭждВCЃК
+
=1(aЃОbЃО0)ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЃЈ0ЃЌcЃЉЁЂF2ЃЈ0ЃЌ-cЃЉЃЈcЃО0ЃЉЃЌХзЮяЯпPЃКx2=2pyЃЈpЃО0ЃЉЕФНЙЕугыF1жиКЯЃЌжЊХзЮяЯпPЃКx2=4cyЃЎЩшЙ§F2ЕФжБЯпlЕФЗНГЬЮЊy+c=kxЃЌСЊСЂ
ЃЌЕУx2-4kcx+4c2=0ЃЌРћгУЮЄДяЖЈРэФмжЄУїЧаЯпlЕФаБТЪЮЊЖЈжЕЃЎ
ЃЈ2ЃЉЩшEO=tЃЌгЩ
=ІЬ(
+
)ЃЌІЬЁЪ(0ЃЌ
)ЃЌжЊTдкЯпЖЮEOЩЯвЦЖЏЃЌЙЪ
ЃЌгЩ
•
ЕФзюаЁжЕЮЊ-
ЃЌЕУЕНt=
ЃЎгЩДЫФмЧѓГіХзЮяЯпPЕФЗНГЬЃЎ
ЃЈ3ЃЉгЩжБЯпlЕФЗНГЬЮЊy=x-
ЃЎСЊСЂ
ЃЌЕУЃЈ2a2-5ЃЉx2-2
ЃЈa2-5ЃЉx-ЃЈa2-5ЃЉ2=0ЃЌЩшAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌдђx1+x2=
ЃЌx1x2=
ЃЎЕБІЫ=2ЪБЃЌx1=-2x2ЃЎЕБІЫ=4ЪБЃЌx1=-4x2ЃЎгЩДЫФмЧѓГіЭждВРыаФТЪeЕФШЁжЕЗЖЮЇЃЎ
| x2 |
| b2 |
| y2 |
| a2 |
|
ЃЈ2ЃЉЩшEO=tЃЌгЩ
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
|
| ET |
| OT |
| 5 |
| 4 |
| 5 |
ЃЈ3ЃЉгЩжБЯпlЕФЗНГЬЮЊy=x-
| 5 |
|
| 5 |
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
НтД№ЃКЃЈ1ЃЉжЄУїЃКЁпЭждВCЃК
+
=1(aЃОbЃО0)ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЃЈ0ЃЌcЃЉЁЂF2ЃЈ0ЃЌ-cЃЉЃЈcЃО0ЃЉЃЌ
ХзЮяЯпPЃКx2=2pyЃЈpЃО0ЃЉЕФНЙЕугыF1жиКЯЃЌ
Ёр
=cЃЌЁрХзЮяЯпPЃКx2=4cyЃЎ
ЩшЙ§F2ЕФжБЯпlЕФЗНГЬЮЊy+c=kxЃЌ
СЊСЂ
ЃЌЕУx2-4kcx+4c2=0ЃЌ
ЁпЙ§F2ЕФжБЯпlгыХзЮяЯпPЯрЧаЃЌЧаЕуEдкЕквЛЯѓЯоЃЌ
Ёр
ЃЌ
НтЕУk=1ЃЎ
ЙЪЧаЯпlЕФаБТЪkЮЊЖЈжЕ1ЃЎ
ЃЈ2ЃЉЩшEO=tЃЌЁп
=ІЬ(
+
)ЃЌІЬЁЪ(0ЃЌ
)ЃЌ
ЁрTдкЯпЖЮEOЩЯвЦЖЏЃЌ
Ёр
ЃЌ
Ёп
•
ЕФзюаЁжЕЮЊ-
ЃЌ
ЁрЕБ|
|=|
|=
ЪБЃЌ
•
ЕФзюаЁжЕ=-
=-
ЃЌ
Ёрt=
ЃЎ
ЁпЙ§F2ЕФжБЯпlгыХзЮяЯпPЯрЧаЃЌЧаЕуEдкЕквЛЯѓЯоЃЌ
ЁргЩЃЈ1ЃЉжЊk=1ЃЌХзЮяЯпдкEЕуДІЕФЕМЪ§ЃЌЕУEЃЈpЃЌ
ЃЉЃЌ
гЩt2=P2+ЃЈ
ЃЉ2=5ЃЌНтЕУP=2ЃЌЫљвдХзЮяЯпЗНГЬЮЊЃЌ
ЁрХзЮяЯпPЕФЗНГЬЮЊx2=4yЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕУc=
ЃЌ
ЁпжБЯпlЕФаБТЪk=1ЃЌЁржБЯпlЕФЗНГЬЮЊy=x-
ЃЎ
СЊСЂ
ЃЌЕУЃЈ2a2-5ЃЉx2-2
ЃЈa2-5ЃЉx-ЃЈa2-5ЃЉ2=0ЃЌ
ЩшAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌдђx1+x2=
ЃЌx1x2=
ЃЎ
ЁпжБЯпlгыЭждВCЯрНЛгкAЁЂBСНЕуЃЌЧв
=ІЫ
ЃЌІЫЁЪ[2ЃЌ4]ЃЌ
ЁрЕБІЫ=2ЪБЃЌx1=-2x2ЃЎ
Ёрx1+x2=
=-x2ЃЌx1x2=
=-2x22ЃЎ
Ёр
=-2•
ЃЌНтЕУa=
ЃЌe=
=
ЃЎ
ЕБІЫ=4ЪБЃЌx1=-4x2ЃЎ
Ёрx1+x2=
=-3x2ЃЌx1x2=
=-4x22ЃЎ
Ёр
=-4•
•
ЃЌНтЕУa=
ЃЌe=
=
ЃЎ
ЁрЭждВРыаФТЪeЕФШЁжЕЗЖЮЇЪЧ[
ЃЌ
]ЃЎ
| x2 |
| b2 |
| y2 |
| a2 |
ХзЮяЯпPЃКx2=2pyЃЈpЃО0ЃЉЕФНЙЕугыF1жиКЯЃЌ
Ёр
| p |
| 2 |
ЩшЙ§F2ЕФжБЯпlЕФЗНГЬЮЊy+c=kxЃЌ
СЊСЂ
|
ЁпЙ§F2ЕФжБЯпlгыХзЮяЯпPЯрЧаЃЌЧаЕуEдкЕквЛЯѓЯоЃЌ
Ёр
|
НтЕУk=1ЃЎ
ЙЪЧаЯпlЕФаБТЪkЮЊЖЈжЕ1ЃЎ
ЃЈ2ЃЉЩшEO=tЃЌЁп
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
ЁрTдкЯпЖЮEOЩЯвЦЖЏЃЌ
Ёр
|
Ёп
| ET |
| OT |
| 5 |
| 4 |
ЁрЕБ|
| ET |
| OT |
| t |
| 2 |
| ET |
| OT |
| t2 |
| 4 |
| 5 |
| 4 |
Ёрt=
| 5 |
ЁпЙ§F2ЕФжБЯпlгыХзЮяЯпPЯрЧаЃЌЧаЕуEдкЕквЛЯѓЯоЃЌ
ЁргЩЃЈ1ЃЉжЊk=1ЃЌХзЮяЯпдкEЕуДІЕФЕМЪ§ЃЌЕУEЃЈpЃЌ
| p |
| 2 |
гЩt2=P2+ЃЈ
| p |
| 2 |
ЁрХзЮяЯпPЕФЗНГЬЮЊx2=4yЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕУc=
| 5 |
ЁпжБЯпlЕФаБТЪk=1ЃЌЁржБЯпlЕФЗНГЬЮЊy=x-
| 5 |
СЊСЂ
|
| 5 |
ЩшAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉЃЌдђx1+x2=
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
ЁпжБЯпlгыЭждВCЯрНЛгкAЁЂBСНЕуЃЌЧв
| F2B |
| AF2 |
ЁрЕБІЫ=2ЪБЃЌx1=-2x2ЃЎ
Ёрx1+x2=
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
Ёр
| -(a2-5)2 |
| 2a2-5 |
| 20(a2-5)2 |
| (2a2-5)2 |
3
| ||
| 2 |
| ||||
|
| ||
| 3 |
ЕБІЫ=4ЪБЃЌx1=-4x2ЃЎ
Ёрx1+x2=
2
| ||
| 2a2-5 |
| -(a2-5)2 |
| 2a2-5 |
Ёр
| -(a2-5)2 |
| 2a2-5 |
| 1 |
| 9 |
| 20(a2-5)2 |
| (2a2-5)2 |
5
| ||
| 6 |
| ||||
|
3
| ||
| 5 |
ЁрЭждВРыаФТЪeЕФШЁжЕЗЖЮЇЪЧ[
| ||
| 3 |
3
| ||
| 5 |
ЕуЦРЃКБОЬтПМВщЧаЯпаБТЪЮЊЖЈжЕЕФЧѓЗЈЃЌПМВщХзЮяЯпЗНГЬЕФЧѓЗЈЃЌПМВщЭждВРыаФТЪШЁжЕЗЖЮЇЕФЧѓЗЈЃЎНтЬтЪБвЊШЯецЩѓЬтЃЌзаЯИНтД№ЃЌзЂвтКЯРэЕиНјааЕШМлзЊЛЏЃЎ

СЗЯАВсЯЕСаД№АИ
 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
ЯрЙиЬтФП
 ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК ШчЭМЃЌвбжЊЭждВCЃК
ШчЭМЃЌвбжЊЭждВCЃК ЃЈ2012•ЩюлквЛФЃЃЉШчЭМЃЌвбжЊЭждВCЃК
ЃЈ2012•ЩюлквЛФЃЃЉШчЭМЃЌвбжЊЭждВCЃК ШчЭМЃЌвбжЊЭждВ
ШчЭМЃЌвбжЊЭждВ