Question

【题目】随着智能手机和电子阅读器越来越普及，人们的阅读习惯也发生了改变，手机和电子阅读产品方便易携带，越来越多的人习惯通过手机或电子阅读器阅读.某电子书阅读器厂商随机调查了人，统计了这人每日平均通过手机或电子阅读器阅读的时间（单位：分钟），由统计数据得到如下频率分布直方图，已知阅读时间在， ， 三组对应的人数依次成等差数列.

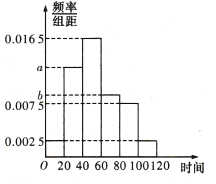
（1）求频率分布直方图中， 的值；

（2）若将日平均阅读时间不少于分钟的用户定义为“电子阅读发烧友”，将日平均阅读时间少于分钟的用户定义为“电子阅读潜在爱好者”，现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出人，再从这人中任取人，求恰有人为“电子阅读发烧友”的概率.

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）由，解得，

又，∴；（2）根据分层抽样方法可得抽取“发烧友”抽取人，“潜在爱好者”抽取人，利用列举法可得这人中任选人的事件有个，其中从人中任取人恰有人为“电子阅读发烧友”的事件共有种，根据古典概型概率公式可得结果.

试题解析：（1）由，

解得，

又，∴.

（2）“电子阅读发烧友”“电子阅读潜在爱好者”的人数之比为： ，所以“发烧友”抽取人，

“潜在爱好者”抽取人，

记事件：从人中任取人恰有人为“电子阅读发烧友”，

设两名“电子阅读发烧友”的人记为： ， ，三名“电子阅读潜在爱好者”的人记为： ， ， ，

则这人中任选人有：

， ， ， ， ， ， ， ， ， ，共种情形，

符合题设条件的有：

， ， ， ， ， 共有种，

因此恰有人为“电子阅读发烧友”的概率为.