题目内容
(本小题满分12分)
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组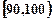 、第二组
、第二组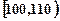 …第六组
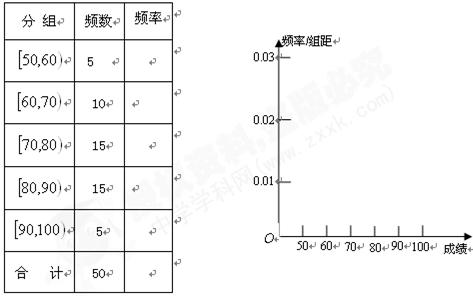
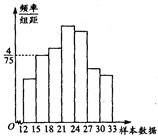
…第六组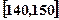 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为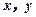 . 若
. 若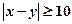 ,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率
,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率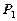 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于120分的人数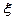 分布列及期望.
分布列及期望.
解:(Ⅰ)设第四,五组的频率分别为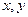 ,则
,则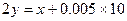 ①
①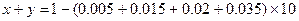 ②由①②解得
②由①②解得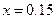 ,
,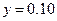 (2分)
(2分)
从而得出直方图(如图所示)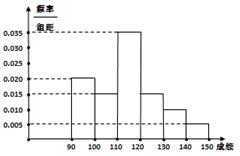
(3分)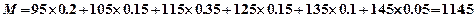 (4分)
(4分)
(Ⅱ)依题意第四组人数为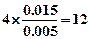 ,故
,故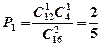 (6分)
(6分)
(Ⅲ)依题意样本总人数为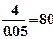 ,成绩不低于120分人数为
,成绩不低于120分人数为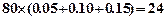 (7分)
(7分)
故在样本中任选1人,其成绩不低于120分的概率为 又由已知
又由已知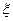 的可能取值为0,1,2,3
的可能取值为0,1,2,3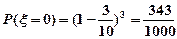 ,
,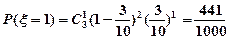 ,
,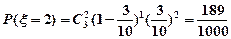 ,
,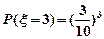 , 故
, 故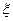 的分布列如下:
的分布列如下:
(10分)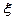
0 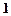
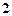
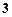
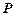
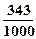
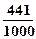
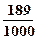
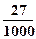
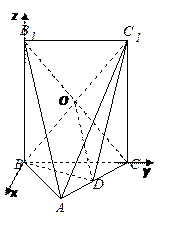 依题意
依题意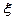 ~
~ .故
.故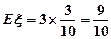
解析

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
、某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天100颗种子的发芽数,如下
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差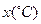 | 10 | 11 | 13 | 12 | 8 |
发芽数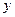 颗 颗 | 23 | 25 | 30 | 26 | 16 |
 求线性回归方程,再用被选取点2组数据进行检验
求线性回归方程,再用被选取点2组数据进行检验(1)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求
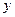 关于
关于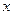 的线性回归方程
的线性回归方程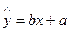 ;
;(2)若线性回归方程得到的估计数据与所选点检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
参考公式:
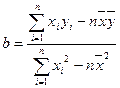 ,
,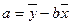
(13分)
某研究机构为了研究人的脚的大小(码)与身高(厘米)之间的关系,随机抽测了20人,得到如下数据:
| 序号 | 身高x | 脚长y | 序号 | 身高x | 脚长y |
| 1 | 176 | 42 | 11 | 179 | 44 |
| 2 | 175 | 44 | 12 | 169 | 43 |
| 3 | 174 | 41 | 13 | 185 | 45 |
| 4 | 180 | 44 | 14 | 166 | 40 |
| 5 | 170 | 42 | 15 | 174 | 42 |
| 6 | 178 | 43 | 16 | 167 | 42 |
| 7 | 173 | 42 | 17 | 173 | 41 |
| 8 | 168 | 40 | 18 | 174 | 42 |
| 9 | 190 | 46 | 19 | 172 | 42 |
| 10 | 171 | 42 | 20 | 175 | 41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成如下2×2列联表;
| | 高个 | 非高个 | 合计 |
| 大脚 | | | |
| 非大脚 | | 12 | |
| 合计 | | | 20 |
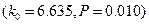
已知x与y之间的一组数据
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
(2)若
 x与y线性相关,写出线性回归方程必定经过的点
x与y线性相关,写出线性回归方程必定经过的点(3)若x与y线性相关求出线性回归方程,
(4)说出2个刻画回归效果的手段,假设R
 =0.74
=0.74 说明什么问题。
说明什么问题。参考公式
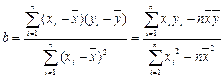

 )根据购买的台数,你认为学校应选择哪家公司更合算?说明理由。
)根据购买的台数,你认为学校应选择哪家公司更合算?说明理由。 依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.
依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.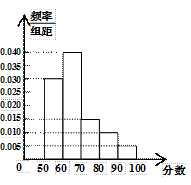
 级的
级的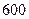 名学生参加一次科普知识竞赛,然后随机抽取
名学生参加一次科普知识竞赛,然后随机抽取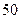 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.