题目内容
2.已知定义在R上的增函数f(x)满足f(x)>0,且对于任意的m,n∈R都有f(m)•f(n)=f(m+n).(1)求f(0)的值;
(2)求证$\frac{f(m)}{f(n)}$=f(m-n)(m,n∈R);
(3)若f(4)=4,且存在x∈[1,t](t>1)使得f(x2)≤$\frac{1}{8}$f(kx),求实数k的取值范围.
分析 (1)利用赋值法,令m=n=0,f(x)>0,解得f0)=′,
(2)令m=m-n,代入计算即可证明,
(3)令m=n=2,求出f(2)=2,原不等式转化为8f(x2)≤f(kx),即为f(6+x2)≤f(kx),根据f(x)在在R上为增函数,得到6+x2≤kx,分离参数,构造函数求出最值,问题得以解决.
解答 解:(1)令m=n=0,
则f(0)f(0)=f(0),
定义在R上的增函数f(x)满足f(x)>0,
∴f(0)=1,
(2)∵f(m)•f(n)=f(m+n),
令m=m-n,
则f(m-n)f(n)=f(m),
∴$\frac{f(m)}{f(n)}$=f(m-n)(m,n∈R);
(3)令m=n=2,则f(2)f(2)=f(4)=4,f(x)>0
∴f(2)=2,
∵f(x2)≤$\frac{1}{8}$f(kx),
∴8f(x2)≤f(kx),
∴f(2)•f(4)f(x2)≤f(kx),
∴f(6+x2)≤f(kx),
∵f(x)在在R上为增函数,
∴6+x2≤kx,
∵x∈[1,t](t>1),
∴k≥$\frac{6}{x}$+x,
令g(x)=$\frac{6}{x}$+x,
则g′(x)=-$\frac{6}{{x}^{2}}$+1=$\frac{{x}^{2}-6}{{x}^{2}}$,
当1<x<$\sqrt{6}$时,g′(x)<0,函数单调递减,
当x>$\sqrt{6}$时,g′(x)>0,函数单调递增,
当1<t<$\sqrt{6}$时,函数g(x)为减函数,
故g(x)min=g(t)=t+$\frac{6}{t}$,
当t≥$\sqrt{6}$时,g(x)在[1,$\sqrt{6}$)上为减函数,在($\sqrt{6}$,t)上为增函数,
故g(x)min=g($\sqrt{6}$)=2$\sqrt{6}$
综上所述,当1<t<$\sqrt{6}$,k≥t+$\frac{6}{t}$,
当t≥$\sqrt{6}$时,k≥2$\sqrt{6}$
点评 本题考查了抽象函数的问题,以及函数的单调性,分类讨论,常常采用赋值法,属于中档题.

| A. | 5+$2\sqrt{2}$ | B. | $8\sqrt{2}$ | C. | 5 | D. | 9 |
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -2 | D. | -$\frac{1}{2}$或-2 |
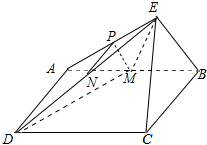 如图,已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.求证:MN⊥EA.
如图,已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.求证:MN⊥EA.