题目内容
16.若不等式x2-2x+k-1>0对x∈R恒成立,则实数k的取值范围是{k|k>2}.分析 不等式x2-2x+k-1>0恒成立,则函数y=x2-2x+k-1的图象都在x轴的上方,得到判别式小于0.
解答 解:∵不等式x2-2x+k-1>0对一切实数x恒成立,
∴△=(-2)2-4(k-1)<0,
解得k>2,
故答案为:{k|k>2}.
点评 本题考查了一元二次不等式恒成立问题求参数范围;关键是与二次函数结合,得到判别式与0的不等式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.函数f(x)=ax3+3x2+3x(a≠0)在区间(1,2)上是增函数,则a的取值范围是( )
| A. | [-$\frac{5}{4}$,0) | B. | (0,+∞) | C. | [-$\frac{5}{4}$,0)∪(0,+∞) | D. | [-$\frac{5}{4}$,0)∪[$\frac{5}{4}$,+∞) |
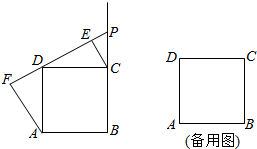 如图,正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C,A作直线DP的垂线,垂足为点E,F.
如图,正方形ABCD中,点P是射线BC上的任意一点(点B与点C除外),连接DP,分别过点C,A作直线DP的垂线,垂足为点E,F.