题目内容
 选修4-1:几何证明选讲
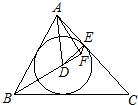
选修4-1:几何证明选讲如图,锐角△ABC的内心为D,过点A作直线BD的垂线,垂足为F,点E为内切圆D与边AC的切点.
(Ⅰ)求证:A,D,F,E四点共圆;
(Ⅱ)若∠C=50°,求∠DEF的度数.
分析:(Ⅰ)证明DE⊥AE,根据AF⊥DF,可得A,D,F,E四点共圆,直径为AD;
(Ⅱ)先证明∠ADB=180°-
=90°+
,再利用A,D,F,E四点共圆,可求∠DEF的度数.
(Ⅱ)先证明∠ADB=180°-
| ∠BAC+∠ABC |
| 2 |
| ∠C |
| 2 |
解答:(Ⅰ)证明:∵点E为内切圆D与边AC的切点,
∴DE⊥AE,
∵AF⊥DF,
∴A,D,F,E四点共圆,直径为AD;
(Ⅱ)∵锐角△ABC的内心为D,∴∠ADB=180°-
=90°+
.
∵∠C=50°,∴∠ADB=115°,
∵∠ADB=90°+∠DAF,
∴∠DAF=25°,
∵A,D,F,E四点共圆,
∴∠DEF=∠DAF=25°.
∴DE⊥AE,
∵AF⊥DF,
∴A,D,F,E四点共圆,直径为AD;
(Ⅱ)∵锐角△ABC的内心为D,∴∠ADB=180°-
| ∠BAC+∠ABC |
| 2 |
| ∠C |
| 2 |
∵∠C=50°,∴∠ADB=115°,
∵∠ADB=90°+∠DAF,
∴∠DAF=25°,
∵A,D,F,E四点共圆,
∴∠DEF=∠DAF=25°.
点评:本题考查四点共圆,考查角的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲