题目内容
 已知全集U=R,集合A={x|-2≤1-x≤0},B={x|y=
已知全集U=R,集合A={x|-2≤1-x≤0},B={x|y=| ln(4-x) | ||
|
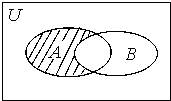
(Ⅰ)求A∪B及Venn图中阴影部分表示的集合D;
(Ⅱ)若集合C={x|4-a<x<a},且C⊆(A∪B),求实数a的取值范围.
分析:(I)通过解不等式求出集合A与集合B,根据阴影部分对应的集合,进行集合运算求得;
(II)先求出集合(A∪B),再由C⊆(A∪B),分C=∅与C≠∅两种情况分类讨论求解.
(II)先求出集合(A∪B),再由C⊆(A∪B),分C=∅与C≠∅两种情况分类讨论求解.
解答:解:(I)A={x|1≤x≤3},
由
⇒2<x<4,B={x|2<x<4}
由题意阴影部分对应集合A∩(CUB),
∵CUB={x|x≥4或x≤2},
∴A∩(CUB)={x|1≤x≤2}.
(II)A∪B={x|1≤x<4},
C={x|4-a<x<a},
当C=∅时,满足C⊆(A∪B),此时a≤4-a,即a≤2;
当C≠∅时,要C⊆(A∪B),则
⇒2<a≤3,
综上,a≤3.
由
|
由题意阴影部分对应集合A∩(CUB),
∵CUB={x|x≥4或x≤2},
∴A∩(CUB)={x|1≤x≤2}.
(II)A∪B={x|1≤x<4},
C={x|4-a<x<a},
当C=∅时,满足C⊆(A∪B),此时a≤4-a,即a≤2;
当C≠∅时,要C⊆(A∪B),则
|
综上,a≤3.
点评:本题考查集合的交、并、补集运算,考查集合的包含关系的判定及应用,求解是要注意空集是任何集合的子集,不要漏解.

练习册系列答案
相关题目