题目内容
11.已知向量$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$.分析 利用向量数量积运算性质、夹角公式即可得出.
解答 解:∵向量$\overrightarrow{a}$=(-1,0),$\overrightarrow{b}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴$|\overrightarrow{a}|$=1,$|\overrightarrow{b}|$=$\sqrt{(\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=1,
$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$.
∴$cos<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-\frac{1}{2}}{1×1}$=-$\frac{1}{2}$,
则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查了向量数量积运算性质、夹角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
1.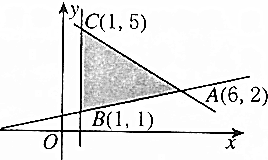 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
 给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )
给出平面可行域(如图),若使目标函数z=ax+y取最大值的最优解有无穷多个,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | 4 | D. | $\frac{5}{3}$ |