题目内容
6.解下列各不等式:(1)|13x|≥7;
(2)|10x|<25;
(3)|x-6|<0.1
(4)3≤|8-x|;
(5)|2x+5|<6;
(6)|4x-1|≥9.
分析 由条件利用绝对值不等式的意义,去掉绝对值,转化为与之等价的不等式来解.
解答 解:(1)|13x|≥7,即|x|≥21,求得它的解集为{x|x≥21,或x≤-21},
(2)|10x|<25,即|x|<125,求得它的解集为{x|-125<x<125}.
(3)|x-6|<0.1,即-0.1<x-6<0.1,求得它的解集为{x|5.9<x<6.1}.
(4)3≤|8-x|,即x-8≥3或 x-8≤-3,求得它的解集为{x|x≥11,或x≤5}.
(5)|2x+5|<6,-6<2x+5<6,即求得它的解集为{x|-112<x<12}.
(6)|4x-1|≥9,即4x-1≥9或 4x-1≤-9,求得它的解集为{x|x≥52,或x≤-2}
点评 本题主要考查绝对值不等式的解法,关键是去掉绝对值,转化为与之等价的不等式,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
16.为了得到函数y=sin(2x−π3)的图象,只需把函数y=cos(2x−π6)的图象( )
| A. | 向左平移π6个单位长度 | B. | 向右平移π6个单位长度 | ||
| C. | 向左平移π3个单位长度 | D. | 向右平移π3个单位长度 |
16.已知平行线3x+2y-6=0和6x+4y-3=0,则与这两条平行线距离相等的点的轨迹是( )
| A. | 3x+2y-4=0 | B. | 3x+2y-5=0 | C. | 6x+4y-9=0 | D. | 12x+8y-15=0 |
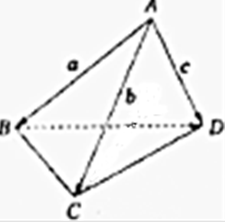 已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.
已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.